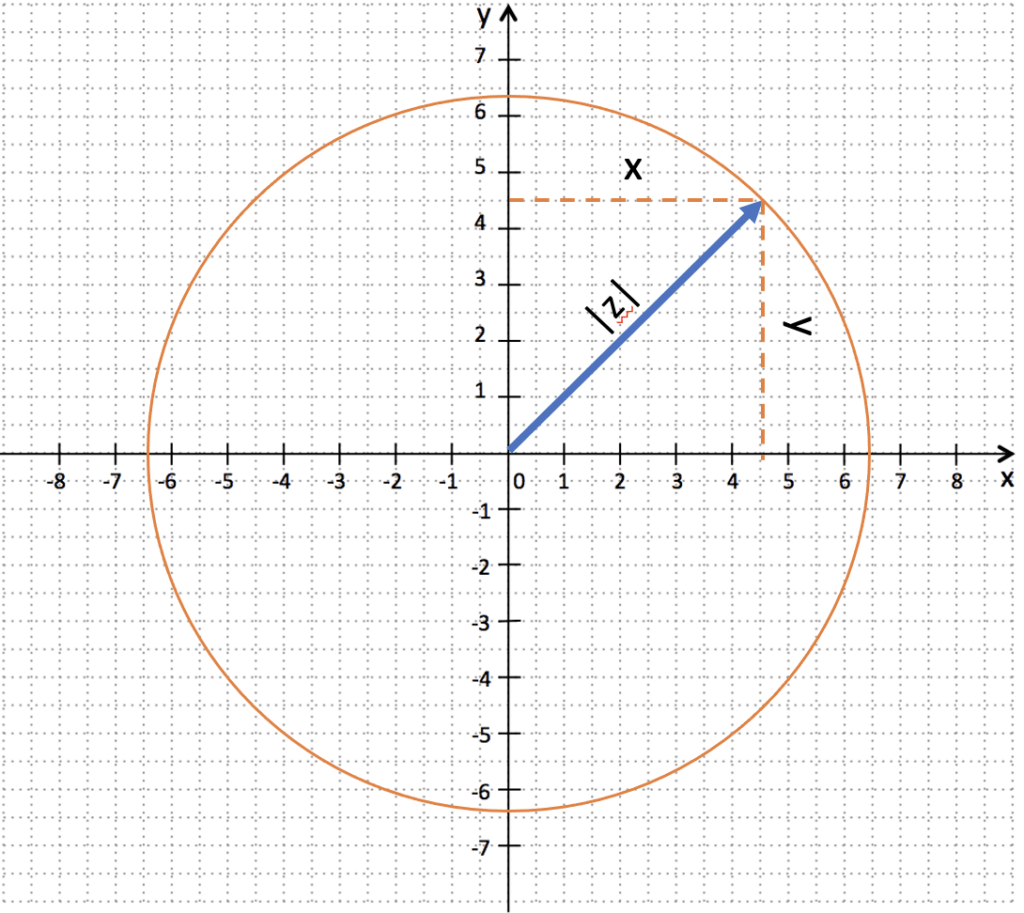
Die Magnitude (Betrag) einer komplexen Zahl gibt ihren Abstand oder ihre Größe vom Ursprung in der komplexen Ebene an. Für eine komplexe Zahl z = x + jy, wobei x den Realteil und y den Imaginärteil darstellt, kann die Magnitude wie folgt berechnet werden:
![]()
Die Magnitude einer komplexen Zahl ist immer ein nicht-negativer Wert. Sie gibt die Länge des Vektors an, der von der Koordinate (x, y) zum Ursprung in der komplexen Ebene verläuft.
Die Magnitude einer komplexen Zahl ist unabhängig von ihrer Phase. Sie gibt nur die Größe des Vektors an und nicht die Richtung oder den Winkel.
Der Betrag des Signals kann z.B. dafür eingesetzt werden, um die Hüllkurve eines Signals zu ermitteln (Envelope Detection).
Dies kann beispielsweise bei der Demodulation von Amplitudenmodulation (AM) verwendet werden, um das modulierte Signal wiederherzustellen.
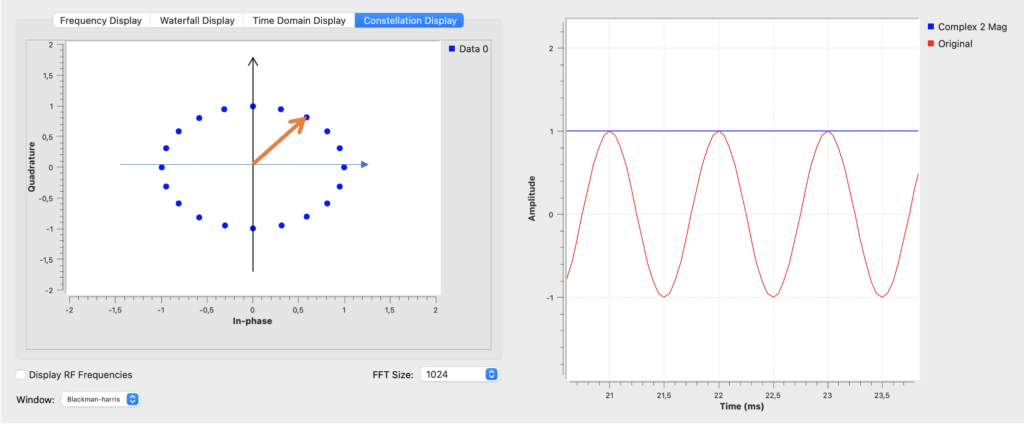
Beispiel 1: Sinussignal mit 1kHz
In diesem Beispiel durchläuft ein 1kHz Sinussignal periodisch die Phase 0..360°. Im Constellation Display sind die einzelnen komplexen Werte dargestellt. Da die Sampling Rate in diesem Beispiel 20kHz beträgt, sind 20 “Messpunkte” im Display enthalten. Bei einer Sinusschwingung ist der Betrag für jeden Messpunkt immer so groß wie die Amplitude des Signals.
Beispiel 2: Rechteck mit 1kHz
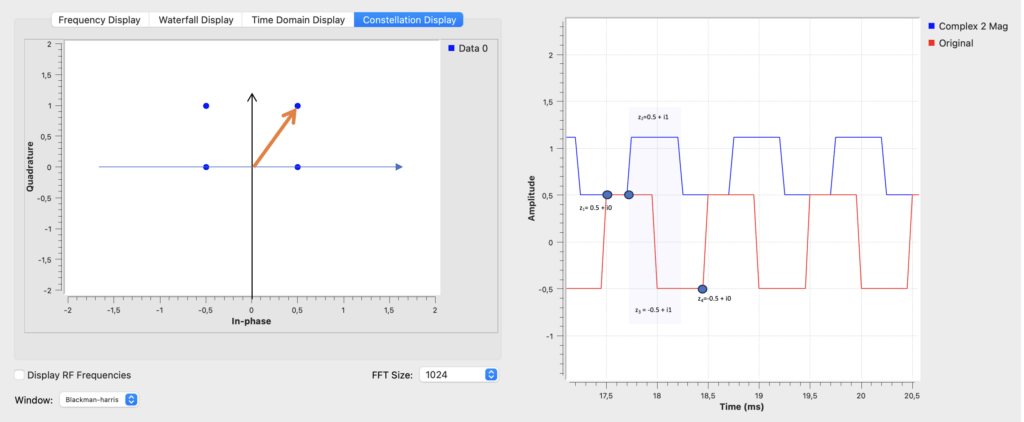
In diesem Bespiel wird ein periodisches Rechteck Signal betrachtet.
Es gibt hier 4 Zustände:
z1 = 0.5 + i0 => |z1| = 0.5
z2 = 0.5 + i1 => |z12| = 1.12
z3 = -0.5 + i1 => |z3| = 1.12
z4 = -0.5 + i0 => |z4| = 0.5