Amplitude Shift Keying (ASK) ist eine Modulationsmethode bei der die Amplitude eines Trägersignals verändert wird, um digitale Informationen zu übertragen.
ASK ist sehr einfach zu implementieren und wird daher oft in einfachen und kostengünstigen Anwendungen mit niedriger Bitrate eingesetzt. Da die Änderungen der Amplitude leicht gestört werden können, ist ASK anfällig für Rauschen und Interferenzen. Es wird daher überwiegend für Anwendungen mit geringer Übertragungsdistanz und geringem Störungspotenzial verwendet.
Beispiele für ASK Anwendungen:
- Fernbedienungen
- Nahfeldkommunikation (NFC)
- Radio Frequency Identification (RFID)
- Übertragung von Messwerten
- Heimautomation
Als Sonderform von ASK kann beim Low-Pegel die Amplitude des Sendesignals auf 0 gesetzt werden. Man spricht in diesem Fall von On-Off Keying (OOK). Bei Verwendung von Morsetelegraphie kommt z.B. OOK zum Einsatz.
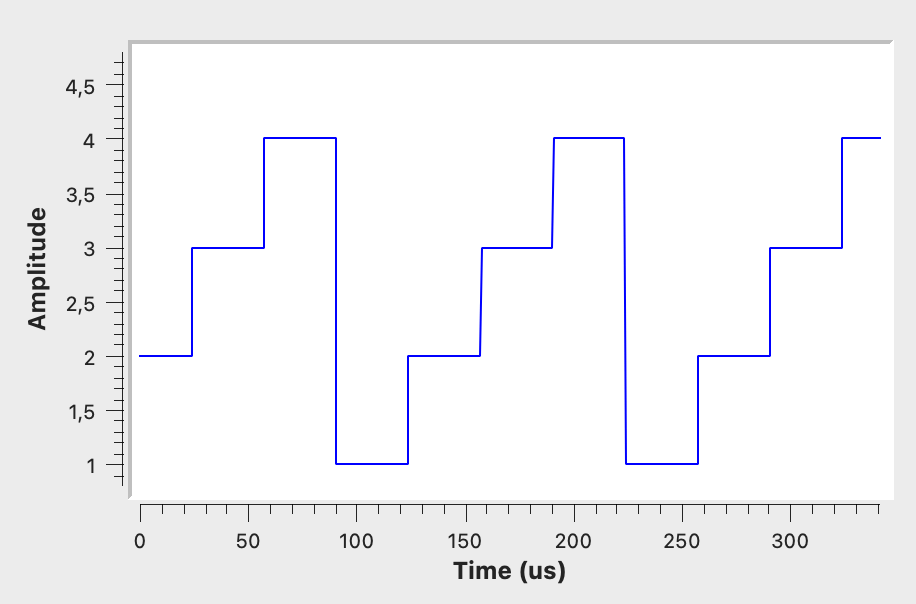
Bei ASK können neben den High und Low Pegeln auch mehrere Amplitudenstufen eingesetzt werden.
Um 2 Bits in einem Schritt zu übertragen kann ASK 4 eingesetzt werden.
Im folgenden Schaubild wurde das Trägersignal mit 4 verschiedenen Amplitudenwerten multipliziert.
Jeder Amplitudenwert stellt einen Signalwert dar.
Bei digitaler Modulation werden Informationen in Form von Symbolen übertragen, wobei jedes Symbol mehrere Bits repräsentiert. Der Begriff Samples per Symbol (SPS) gibt dabei an, wie viele Abtastungen pro Symbol durchgeführt werden, um das Modulationssignal zu erzeugen.
Im Beispiel oben wurden 100 Samples für die Darstellung verwendet.
Ein weiterer Begriff in Zusammenhang mit der SPS Rate ist die Symbolrate. Sie gibt an, wieviele Symbole pro Sekunde übertragen werden.
Dieser Wert ist abhängig von der zu Gunde liegenden Sampling Rate.
Bei einer Samplingrate von 3MHz und einer SPS von 100, können 30000 Symbole pro Sekunde übertragen werden.
Mit Hilfe des folgenden Python Programms wurde ein ASK Signal erzeugt, das in einer Sequenz die Werte 0,1,2,3 sendet.
import numpy as np
import matplotlib.pyplot as plt
# Parameter definieren
bit_rate = 5000 # Bitrate in Hz
carrier_freq = 10e3 # Trägerfrequenz in Hz
sample_rate = 100e3 # Abtastfrequenz in Hz
sequence = [0, 1, 2, 3] # Werte, die wiederholt werden sollen
repeats = 3 # Anzahl der Wiederholungen der Sequenz
duration_per_bit = 1 / bit_rate # Dauer eines Bits
samples_per_bit = int(sample_rate * duration_per_bit) # Abtastpunkte pro Bit
def generate_ask_signal(sequence, carrier_freq, sample_rate, samples_per_bit, modulation_index=1):
t = np.linspace(0, duration_per_bit, samples_per_bit, endpoint=False) # Zeitpunkte für ein Bit
carrier = np.sin(2 * np.pi * carrier_freq * t) # Trägersignal
# Skalierte Amplituden basierend auf dem Modulationsindex
A_min = 0 # Minimale Amplitude (unmoduliertes Signal)
A_max = max(sequence) # Maximale Amplitude
amplitude_scaling = lambda A: (modulation_index ) * (A - A_min)
signal = []
for value in sequence:
effective_amplitude = amplitude_scaling(value) # Skaliere die Amplitude
modulated = effective_amplitude * carrier # ASK-Modulation
signal.extend(modulated)
return np.array(signal)
# Wiederhole die Sequenz
extended_sequence = sequence * repeats
# ASK-Signal generieren
ask_signal = generate_ask_signal(extended_sequence, carrier_freq, sample_rate, samples_per_bit)
# Zeitachse für das gesamte Signal
signal_duration = len(extended_sequence) * duration_per_bit
t = np.linspace(0, signal_duration, len(ask_signal), endpoint=False)
# Plotten des Signals
plt.figure(figsize=(10, 4))
plt.plot(t, ask_signal)
plt.title("ASK-Signal")
plt.xlabel("Zeit (s)")
plt.ylabel("Amplitude")
plt.grid()
plt.show()Es ergibt sich folgendes Signal:
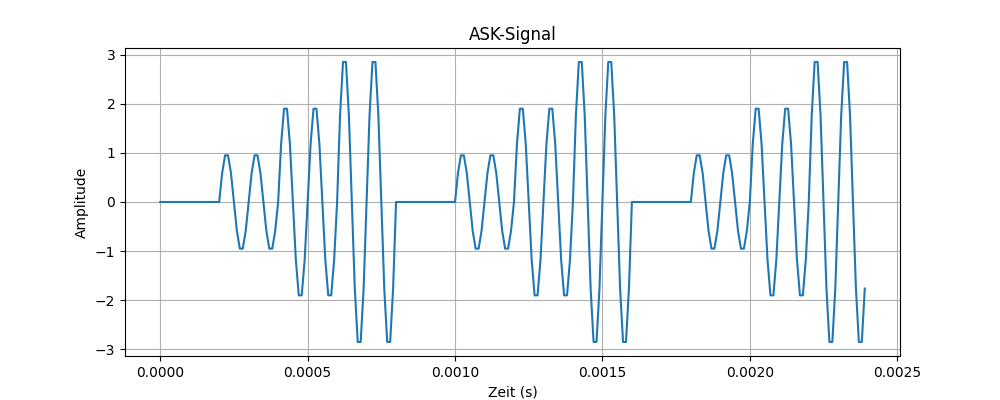
Die Trägerfrequenz beträgt 10kHz und die Bitrate 5kHz. Ein Bit hat daher 2 Schwingungen der Trägerfrequenz. Nimmt man an, dass jedes zu übertragende Symbol mit 4 Bit verschlüsselt ist, ergibt sich eine Symbol Rate von 5kHz/4 = 1250Hz
Die Bitrate muss wieder das Nyquist Kriterium erfüllen, da dies sonst zu Inter-Symbol-Interferenz (ISI) führt, bei der die Bits sich gegenseitig beeinflussen.. Die Trägerfrequenz muss also mindestens doppelt so hoch wie die Bitrate sein.
In der Praxis sollte die Trägerfrequenz deutlich höher als die Bitrate sein (oft 10-mal oder mehr), um saubere Übergänge und klare Trennung der Bits im Frequenzspektrum sicherzustellen
DEMODULATION
Die Demodulation des ASK Signals erfolgt wie bei der AM Demodulation z.B.durch den Einsatz des Complex to Mag Blocks, um die Energie des Signals zu berechnen und den Threshold Block, um die jeweilige Stufe zu ermitteln. Um unten aufgeführten Beispiel ist neben der Schwellwert Methode auch eine Korrekationsmethode für die Demodulation dargestellt.
Um ein ASK Signal zu demodulieren, ist es normalerweise notwendig, die Symbolrate zu kennen. Es kann sonst nicht unterschieden werden, ob ein einzelnes Symbol oder mehrere gleiche Symbole übertragen werden.
In einigen Kommunikationssystemen kann das SPS-Verhältnis angepasst werden, um sich an Änderungen der Kanalbedingungen anzupassen. Dies wird als adaptive Modulation bezeichnet und ermöglicht eine optimale Nutzung des Kanals. Die Symbolrate muss, sofern der Sender keine anderweitigen Informationen zur Verfügung stellt, durch die Analyse des Signals ermittelt werden. Dies kann durch das Erkennen von Symbolen im Signal, das Messen der Zeitdauer zwischen aufeinanderfolgenden Symbolen oder das Verwenden von spezieller Software oder Algorithmen erfolgen.
Beispiel der Demodulation mittels Python
Für die Demodulation des o.a. Python Signals kann die Demodulation auch mittels einer Art Korrelation erfolgen. Vereinfacht gesagt, wird ein Signal dabei mit einem Referenzsignal verglichen und die Ähnlichkeit zwischen den Signalen ermittelt. In unserem Beispiel gibt es Referenzsignale für eine 0,1,2 und 3. Ist die Übereinstimmung nach der Korrelation hoch, so kann man annehmen, dass der entsprechende Wert gesendet wurde.
# Demodulation des ASK-Signals mittels Korrelation
def demodulate_ask_signal(ask_signal, carrier_freq, sample_rate, samples_per_bit, possible_values):
t = np.linspace(0, duration_per_bit, samples_per_bit, endpoint=False) # Zeitpunkte für ein Bit
carrier = np.sin(2 * np.pi * carrier_freq * t) # Trägersignal
num_bits = len(ask_signal) // samples_per_bit # Anzahl der Bits im Signal
demodulated_sequence = []
for i in range(num_bits):
start = i * samples_per_bit
end = start + samples_per_bit
segment = ask_signal[start:end]
# Korrelieren mit dem Trägersignal
correlation = np.dot(segment, carrier)
energy = np.sum(carrier ** 2) # Energie des Trägersignals
amplitude = correlation / energy # Normierte Amplitude
# Finde den nächsten Wert aus den möglichen Amplituden
closest_value = min(possible_values, key=lambda x: abs(x - amplitude))
demodulated_sequence.append(closest_value)
return demodulated_sequence
# Mögliche Werte für die Demodulation
demodulation_values = [0, 1, 2, 3]
# ASK-Signal demodulieren
demodulated_sequence = demodulate_ask_signal(ask_signal, carrier_freq, sample_rate, samples_per_bit, demodulation_values)
print("Original Sequence:", extended_sequence)
print("Demodulated Sequence:", demodulated_sequence)np.dot(a, b) berechnet das Skalarprodukt des modulierten Signals und der Trägerfrequenz (inneres Produkt). Das Ergebnis gibt an, wie stark das modulierte Signal dem Trägersignal entspricht, was proportional zur ursprünglichen Amplitude ist. Diese Funktion fürht die Korrelation durch.
Weiterhin wird die Energie des Trägersignals berechnet, die als Referenz verwendet wird, um die Amplitude zu normalisieren. Die Energie ist die Summe der quadrierten Werte des Trägersignals.
Dividiert man den Wert aus der Korrelation durch die Energie des Trägersignals, erhält man die normierte Amplitude des empfangenen Signals.
Es wird nun verglichen, welchem Wert die normierte Amplitude am ehesten entspricht. Das ist das demodulierte Signal.
Anstatt der Verwendung der Korrelationsmethode, kann auch eine einfachere Analyse des Signals mittels Schwellwerten erfolgen. Die Bits sind in unserem Signal durch 4 Amplitudenstufen repräsentiert. Diese können auch durch die Verwendung von Schwellwerten für jedes Bit ermittelt werden.
Auch in diesem Verfahren wird die Energie des Trägersignals in Relation zur Energie des empfangenen Signals gesetzt.
Der Energieansatz berücksichtigt die gesamte Leistung des Signals über die Zeit und ist daher robuster gegenüber kleinen Schwankungen und verrauschten Signalen.
Hier wird deutlich, dass der Amplitudenabstand (Amplitude Spacing) für die korrekte Ermittlung des Bits insbesondere bei verrauschten Signalen von Bedeutung ist, da ein Rauschen den Schwellwert zum nächsten Bit ggf. überschreiten kann.
In ASK wird Modulationsindex basierend auf der maximalen und minimalen Amplitude für das Signal berechnet:
m = (Amax – Amin) / (Amax + Amin)
Ein Modulationsindex von m=1 bedeutet, dass die Amplitude vollständig zwischen dem Minimum (0) und dem Maximum (3) schwingt. Dies ist typisch für ein ASK-Signal, bei dem die gesamte Spannweite der Amplituden genutzt wird.
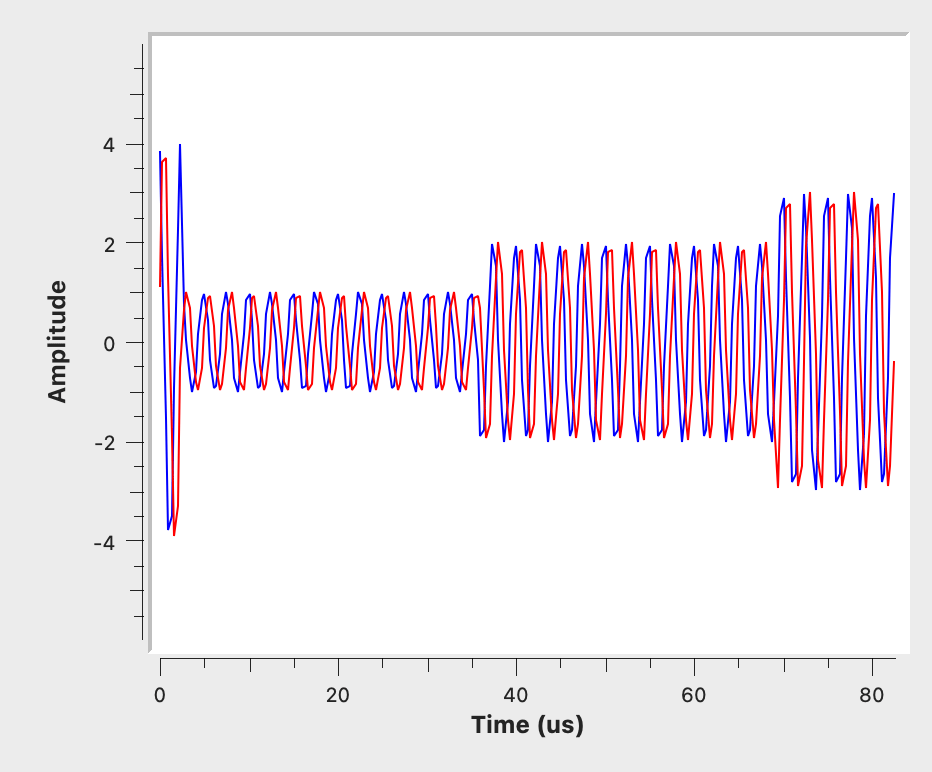
Im folgenden Beispiel wurde zusätzlich Rauschen in das Signal eingefügt
# Rauschen erzeugen
mean = 0 # Mittelwert der Normalverteilung
std_dev = 0.2 # Standardabweichung der Normalverteilung (beeinflusst die Rauschstärke)
noise = np.random.normal(mean, std_dev, len(ask_signal))Damit verändert sich das Signal wie folgt:
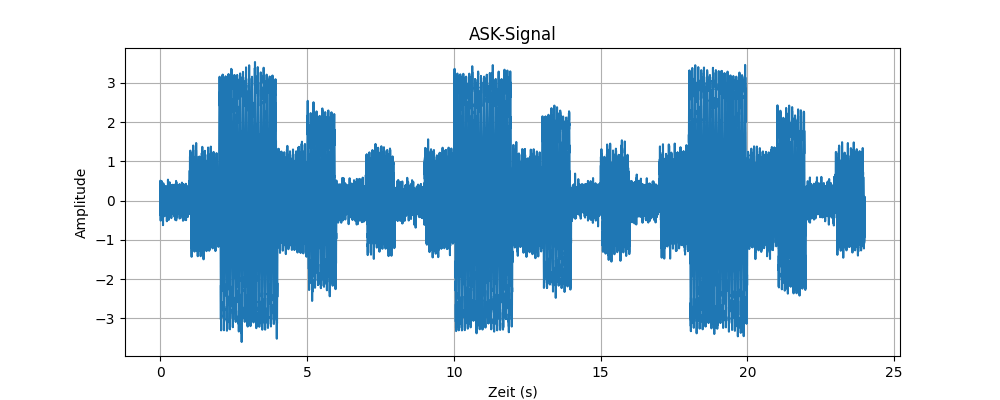
Die Ergebnisse der Demodulation im Vergleich zum Ausgangssignal sind unten aufgeführt.
| Original Sequence: | [0, 1, 3, 3, 1, 2, 0, 1, 0, 1, 3, 3, 1, 2, 0, 1, 0, 1, 3, 3, 1, 2, 0, 1] |
| Demodulated Sequence: | [0, 1, 3, 3, 1, 2, 0, 1, 0, 1, 3, 3, 1, 2, 0, 1, 0, 1, 3, 3, 1, 2, 0, 1] |
| Demodulated Sequence with Threshold: | [0, 1, 3, 3, 1, 3, 0, 1, 0, 1, 3, 3, 1, 3, 0, 1, 0, 1, 3, 3, 1, 3, 0, 1] |
Wie man sieht, ist bei der Threshold Variante ein Bitfehler aufgetreten.