Die folgende Flowchart dient dazu einfaches Sinussignal darzustellen
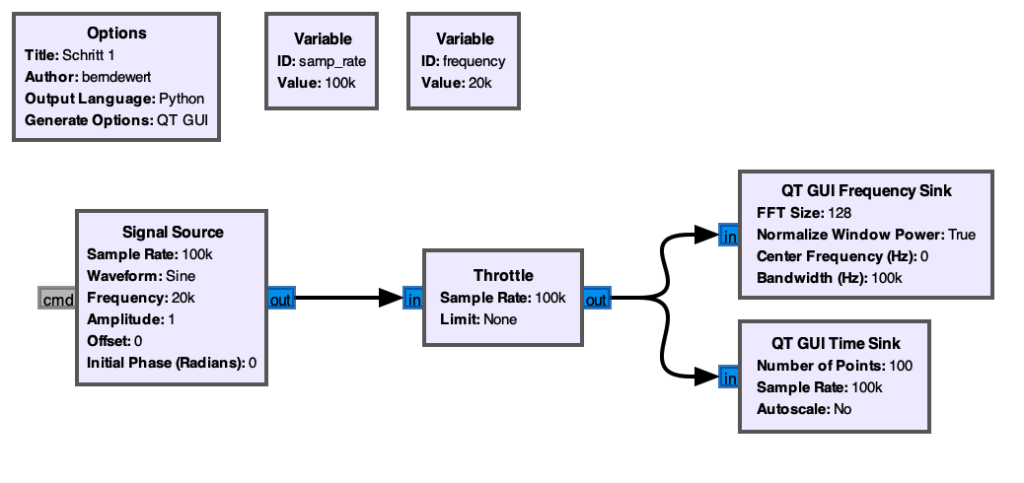
Die Signalquelle liefert ein Sinus Signal mit 20kHz.
Der Throttle Block dient der Limitierung des Eingangssignals.
Die GUI Blöcke liefern ein Ausgangssignal im Zeit und Frequenzbereich.
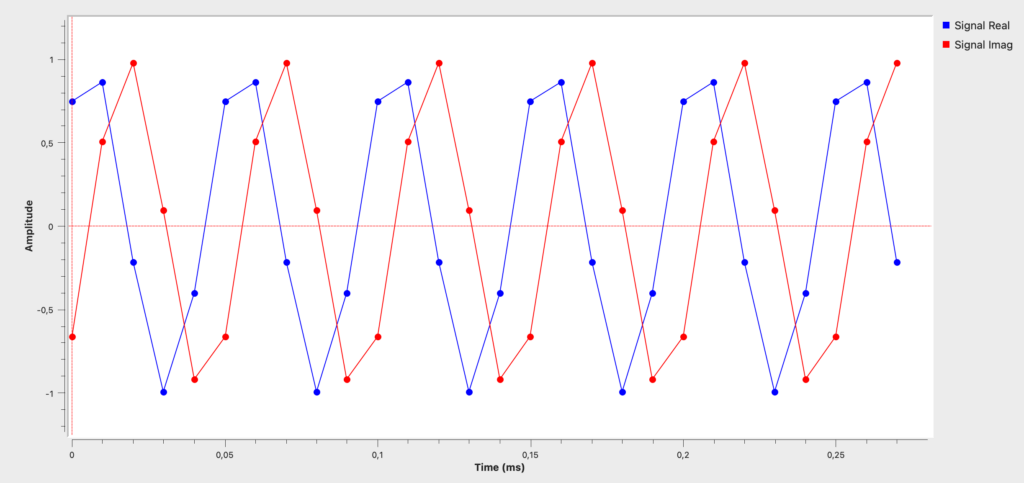
Signal im Zeitbereich
Da wir als Signaloutput „Complex“ gewählt haben, werden beide Signalanteile (I und Q) im Zeitbereich dargestellt. Das rote Signal (Q) ist dabei um 90° phasenverschoben.
Bei einer Frequenz von 20 kHz und einer Samplerate von 100 kHz werden 5 Messpunkte (100/20) pro Periode generiert. Diese Punkte sind auf der Kurve markiert.
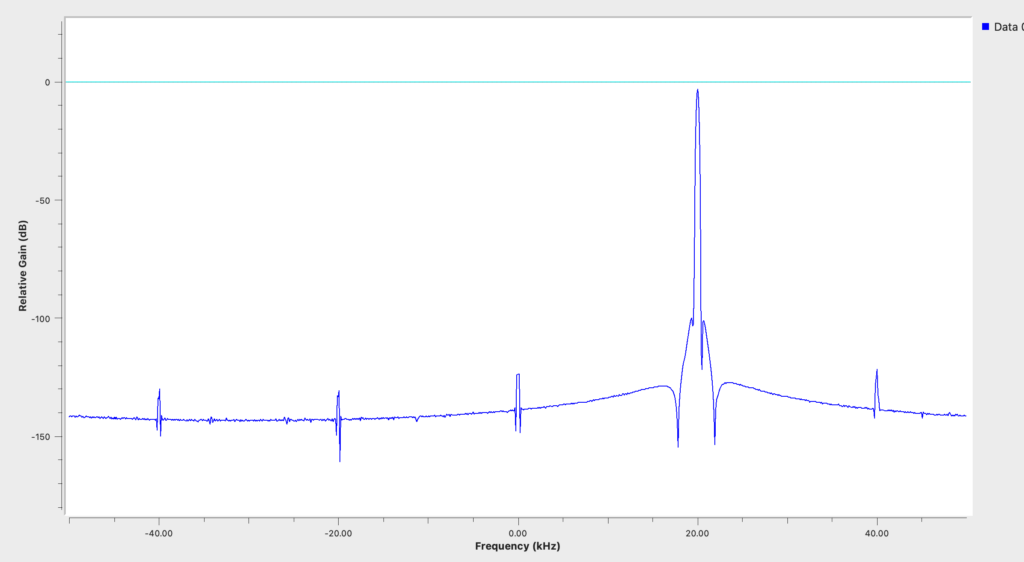
Signal im Frequenzbereich
Das Spektrum des Signals zeigt bei 20 kHz einen Peak. Eigentlich würde man hier nur einen einzelnen Strich bei 20 kHz erwarten, da es sich um ein Sinus-Signal mit fester Frequenz handelt. Da wir jedoch mit diskreten Signalen arbeiten und die Fourier-Transformation mit einer definierten Anzahl von Werten (hier 1024) durchgeführt wird, kann die Frequenz nicht vollständig exakt wiedergegeben werden. Die Ausgabe des Signals wird zudem durch die Wahl des Fenstertyps beeinflusst. Hier wird das Blackman-Harris-Fenster verwendet, eine häufig in der Spektralanalyse eingesetzte Fensterfunktion, um die Auswirkungen der Fensterung auf das Frequenzspektrum zu minimieren und die Leistungsspektren von Signalen genauer zu erfassen.
Das dargestellte Spektrum weist einige Besonderheiten auf, die nicht sofort ersichtlich sind.
Während das eigentliche Signal bei 20 kHz korrekt dargestellt ist, treten auch negative Frequenzanteile auf. In der „realen“ Welt existieren keine negativen Frequenzen, aber in der Mathematik der komplexen Zahlen entstehen diese. Beim Software Defined Radio (SDR) wird das zu analysierende Signal vom Spektrum (durch die Bandbreite, die durch das Sampling festgelegt ist) zum Nullpunkt des Koordinatensystems verschoben. Im Nullpunkt liegt die gewählte Mittelfrequenz. Daher entstehen rechts und links der Mittelfrequenz Signalanteile, wobei die eine Hälfte zwangsläufig negativ ist.
Im Spektrum erscheinen außerdem Vielfache der Mittelfrequenz. Dies ist auf die mathematischen Eigenschaften der diskreten Fourier-Transformation (DFT) zurückzuführen. Da nur eine endliche Anzahl von Frequenzpunkten (hier 1024) für die DFT verwendet wird, wird angenommen, dass sich dieser Abschnitt des Signals periodisch wiederholt. Dadurch wird auch das Frequenzspektrum periodisch, wobei die Wiederholungsfrequenz durch die Abtastrate des Signals bestimmt wird.
Bei der DFT wird das Zeitbereichssignal in diskrete Frequenzbänder aufgeteilt. Die Anzahl dieser Bänder wird durch die Anzahl der verwendeten Werte bestimmt, die üblicherweise eine Potenz von 2 sind (z. B. 1024, 2048, 4096 usw.). Diese Anzahl wird auch als FFT-Größe (Fast Fourier Transform) bezeichnet und kann im Frequenz-Sink-Block eingestellt werden.
Eine größere FFT-Größe ermöglicht eine feinere Frequenzauflösung im Spektrum, da mehr diskrete Frequenzpunkte berechnet werden. Dadurch werden auch die harmonischen Komponenten des Signals präziser dargestellt.
Eine kleinere FFT-Größe führt hingegen zu einer geringeren Auflösung im Frequenzbereich und kann dazu führen, dass harmonische Komponenten weniger genau oder gar nicht sichtbar sind.
Die Wahl der richtigen FFT-Größe ist daher entscheidend, um die gewünschte Auflösung und Genauigkeit im Frequenzbereich zu erzielen und die harmonischen Komponenten des Signals angemessen darzustellen. Eine ausreichend große FFT-Größe ermöglicht eine präzisere Analyse und Identifikation der harmonischen Struktur eines Signals im Spektrum.
Im FFT-Diagramm steht „relative Gain“ für den relativen Verstärkungsgrad eines Frequenzbereichs im Vergleich zu anderen Frequenzbereichen. Es gibt an, wie stark eine bestimmte Frequenzkomponente im Vergleich zu anderen Frequenzen verstärkt oder abgeschwächt wird.
Ein relativer Gain von 0 dB bedeutet, dass die Frequenzkomponente weder verstärkt noch abgeschwächt wird. Positive Werte deuten auf eine Verstärkung hin, während negative Werte eine Abschwächung anzeigen.
Ein Abschwächungswert von -100 dB bedeutet, dass das Signal um 100 Dezibel abgeschwächt wurde. Dezibel (dB) ist eine logarithmische Maßeinheit, die das Verhältnis von zwei Größen, wie beispielsweise Amplituden oder Leistungen, beschreibt.
Ein Wert von -100 dB zeigt eine erhebliche Abschwächung an, bei der das Signal um den Faktor 10^(-10) reduziert ist.
Daher haben die Spektralanteile neben der Mittelfrequenz nur einen geringen Einfluss auf das Hauptsignal.