Reelle Zahlen sind die gewöhnlichen Zahlen, mit denen wir im Alltag vertraut sind. Reelle Zahlen haben einen einzigen Wert und werden zur Darstellung von Größen verwendet, die keine Phasenverschiebung oder komplexe Eigenschaften aufweisen. In der Elektrotechnik werden reelle Zahlen verwendet, um Größen wie Spannung, Stromstärke, Widerstand und Leistung zu beschreiben.
Komplexe Zahlen bestehen aus zwei Teilen: einem Realteil und einem Imaginärteil. Sie werden in der Form z = a + bi dargestellt, wobei a der Realteil ist, b der Imaginärteil und i die imaginäre Einheit (i = √(-1)) ist. Komplexe Zahlen werden verwendet, um Größen zu beschreiben, die eine Phasenverschiebung oder komplexe Eigenschaften aufweisen, wie beispielsweise Wechselstrom und Signale in der Frequenzdomäne. Komplexe Zahlen ermöglichen die Darstellung von Signalen mit Amplitude und Phase und sind daher besonders nützlich bei der Analyse von Schwingungen, Phasenverschiebungen und der Lösung von komplexen elektrischen Schaltungen.
I/Q-Zahlen sind eine spezielle Art von komplexen Zahlen, die verwendet werden, um Signale in der digitalen Signalverarbeitung zu beschreiben. I/Q-Zahlen bestehen aus einem Inphase-Anteil (I) und einem Quadratur-Anteil (Q) und werden in der Form z = I + jQ dargestellt, wobei j die imaginäre Einheit (j = √(-1)) ist.
I/Q-Zahlen sind Teil des komplexen Zahlenraums und ermöglichen die Darstellung von Signalen mit Amplitude, Phase und einer zeitlichen Verzögerung (Phasenverschiebung) zwischen den I- und Q-Komponenten. Der SDR Empfänger liefert die abgetasteten Werte des Signals als I/Q Daten. Dazu liefert der A/D Wandler des SDR Empfängers pro Sample 2 Werte zurück. Im ersten Wert ist die In-Phase-Komponente (I) und im zweiten die Quadratur-Komponente (Q).
In-Phase-Komponente (I): Sie bildet das ursprüngliche Signal ohne Phasenverschiebung ab und erfasst so die Amplitudenänderungen des Signals in der gleichen Phase wie die Referenz. Die Referenz ist normalerweise ein lokaler Oszillator.
I * cos(⍵t)
Quadraturkomponente (Q): Sie bildet die Abweichungen des ursprüngliche Signals mit einer Phasenverschiebung von 90 Grad (π/2) im Vergleich zur gleichphasigen Komponente ab. Auch hier kommt ein Referenzsignal aus dem lokalen Oszillator zum Einsatz
Q * sin(⍵t)
Die Phasenverschiebung zwischen dem I und Q Signal vom 90° ist eine der Grundeigenschaften von komplexen Zahlen. Mathematisch gesehen sind eine Sinus – und eine Cosinus-Funktion um eine viertel Periode also π/2 = 90° verschoben.
Das IQ Signal entsteht durch die Addition der beide Komponenten:
y(t) = I * cos(⍵t) + Q * sin(⍵t)
Durch die Veränderung des Betrages von I und / oder Q verändern sich die Eigenschaften des resultierenden Signals:
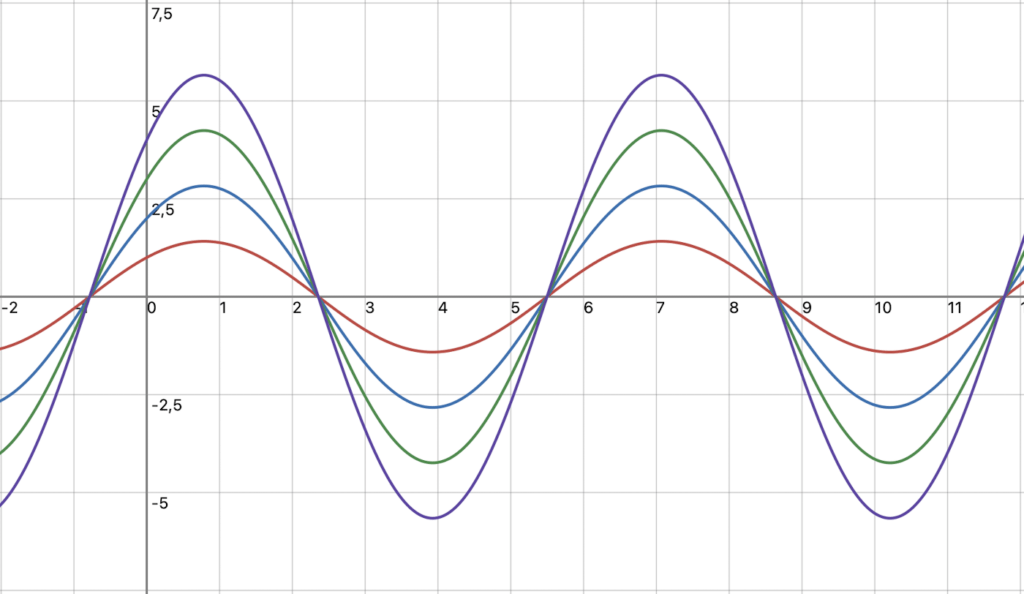
In diesem Beispiel ist der Betrag von I und Q gleich.
Eine gleichmäßige Veränderung bewirkt eine Änderung der Amplitude des resultierenden Signals.
y(t) = n*I * cos(⍵t) + n*Q * sin(⍵t)
Man erhält eine Amplitudenmodulation.
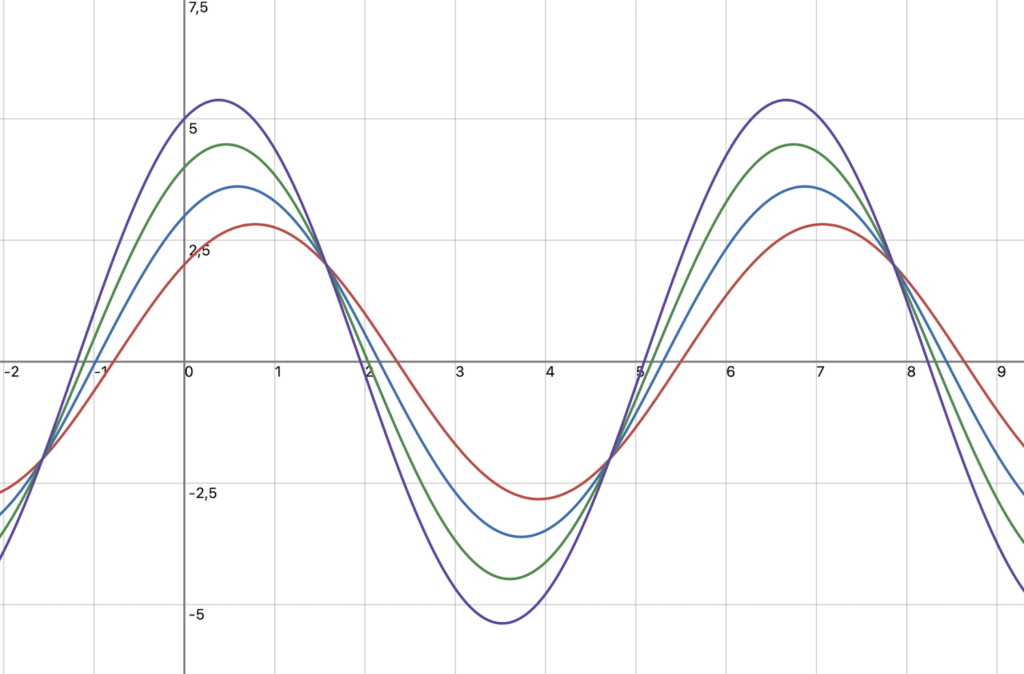
Hier wird I und Q in unterschiedlichem Maße verändert
y(t) = I * cos(⍵t) + n*Q * sin(⍵t)
Man erhält einer Phasenverschiebung des Signals. Dies entspricht einer Phasenmodulation.
Für die Demodulation z.B. einer AM (Amplituden Modulation) Aussendung, bei der das Nutzsignal lediglich die Amplitude des Signals moduliert, wäre die Q-Komponente des Signals nicht zwingend notwendig. Bei komplexeren Modulationstechniken (z.B. QAM oder QPSK) wird jedoch sowohl der I als auch der Q Teil des Signals benutzt, um Informationen abzubilden. Durch die Kombination von AM und PM (Phasenmodulation) erreicht man eine Orthogonalität, bei der 2 Informationen gleichzeitig und unabhängig voneinander im Signal enthalten sein können.
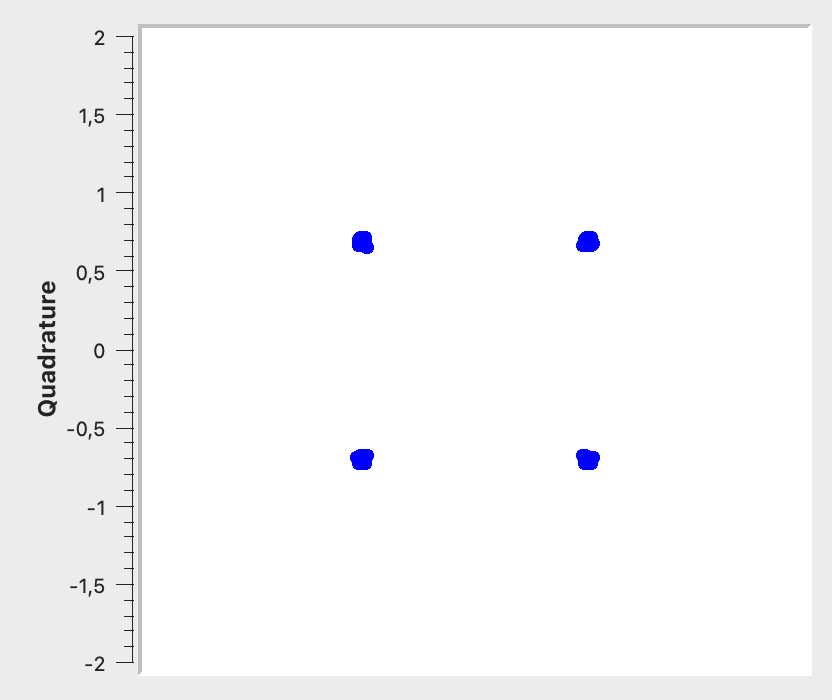
Constellation Diagramm
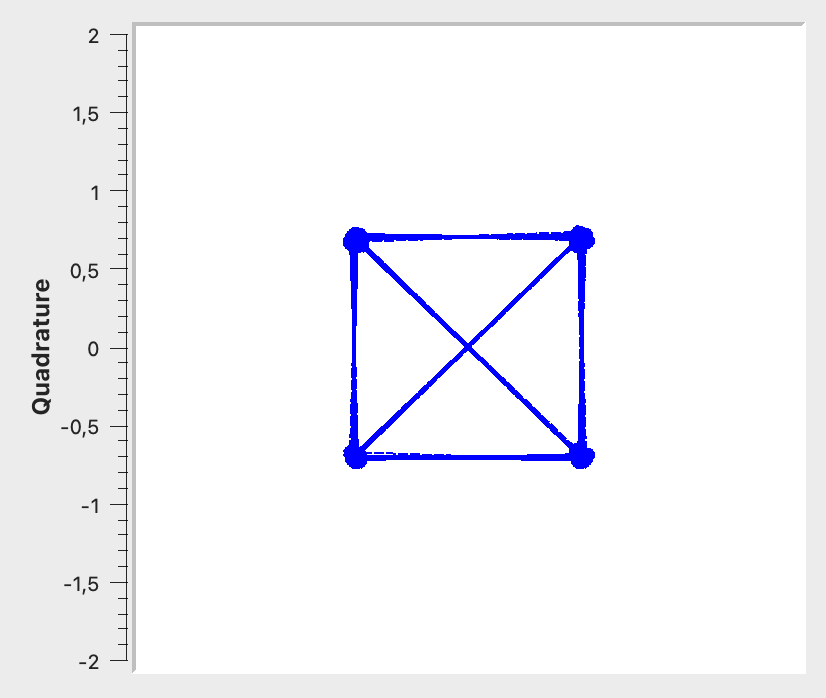
IQ -Werte können im sogenannten Constellation Diagramm dargestellt werden. Insbesondere bei der Betrachtung von digital modulierten Signalen, kann so festgestellt werden, welche Zustände das Signal im komplexen Zahlenraum einnimmt. Analoge Signale verändern die Phase eines Signals normalerweise kontinuierlich, bei phasenmodulierten, digitalen Signalen nehmen bestimmte Bitkombinationen bestimmte Amplituden- und Phasenzustände ein. Diese Zustände werden im Constellation Diagramm als Punktwolken (durch das Rauschen) dargestellt.
Verbindet man die einzelnen Punkte miteinander, so erhält man ein Vektor Diagramm. Dies gibt zusätzlich Aufschluss darüber, in welcher Reihenfolge die einzelnen komplexen Werte eingenommen werden.