Komplexe Zahlen

Für die mathematische Darstellung von IQ Signalen kommen in der Mathematik die komplexen Zahlen zum Einsatz.

Komplexe Zahlen sind eine Erweiterung der bekannten reellen Zahlen und bestehen aus einer reellen Komponente und einer imaginären Komponente. Eine komplexe Zahl wird in der Form z = x + yi dargestellt, wobei x die reelle Komponente ist, y die imaginäre Komponente und i die imaginäre Einheit (manchmal wird statt dem i auch j geschrieben), die definiert ist als die Quadratwurzel von -1.
Die Wurzel aus einer negativen Zahl ist im reellen Zahlenraum nicht definiert. Bei den komplexen Zahlen ist die Berechnung definiert
und i² = -1

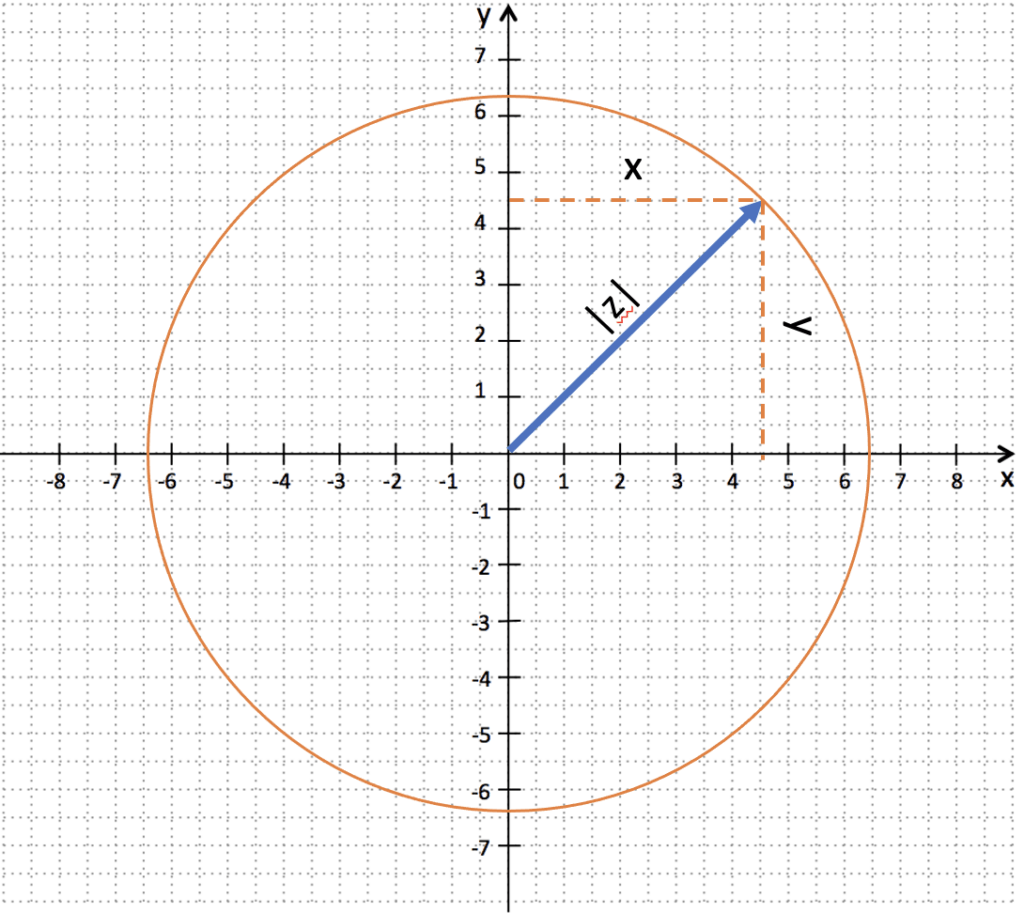
Eine Komplexe Zahl kann in einem Diagramm dargestellt werden, wobei x den Wert auf der x-Achse (auch Realachse genannt) angibt und y , die imaginäre Komponente auf der y-Achse (auch Imaginärachse genannt).

In der komplexen Ebene wird die komplexe Zahl z als Punkt dargestellt, der die Koordinaten (x, y) hat.

Die Länge des Vektors vom Mittelpunkt bis zum Punkt(x,y) ist der Betrag bzw. die Magnitude der komplexen Zahl.

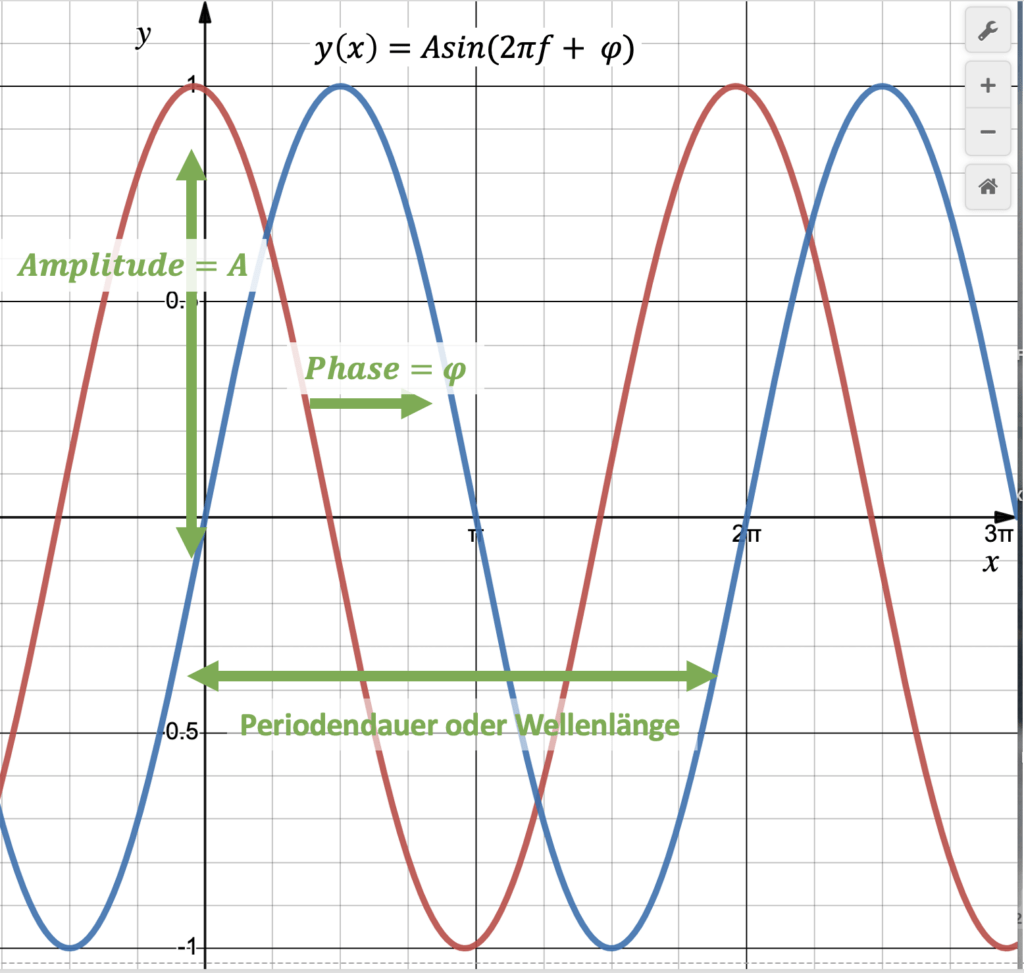
Eine Sinuskurve ist quasi der Ausgangspunkt für das Verständnis der komplexen Zahlen.

Das folgende Bild zeigt die 3 wichtigsten Komponenten einer Sinuskurve:

1. Amplitude (hier der Spitzenwert der Sinusschwingung)
2. Frequenz. In der Funktion ist sie als Kreisfrequenz ⍵ = 2πf dargestellt.
3. Phase (hier Anfangsphase) ϕ

Eine Cosinuskurve lässt sich allgemein wie folgt darstellen:

M*cos(⍵t + ϕ) = A*cos(⍵t) + B*sin(⍵t),

Eine weitere Form der Darstellung findet man oft in den mathematischen Formeln z.B. zur Fouriertransformation:

A*cos(⍵t) + B*sin(⍵t) lässt dich dabei als komplexe Zahl in
der Form z = I + jQ darstellen (unsere IQ Darstellung).

M*cos(⍵t + ϕ) entspricht dann Mag*e^jϕ

Der Wert für Mag wird auch als Magnitute bzw. Betrag der komplexen Zahl bezeichnet. In SDR gibt es einen eigenen Block für die Berechnung der Magnitude.e^j⍵t lässt sich auch in der Form cos(⍵t ) * j sin(⍵t )

Es gibt eine Reihe von Blöcken, die die mathematischen Berechnungen mit komplexen Zahlen erledigen.

Neben Addition und Multiplikation ist z.B. auch die Ermittlung des Betrages mit dem Block Complex to Mag möglich.

Bei den Blöcken muss zudem teilweise angegeben werden, ob mit reellen oder Komplexen Zahlen gerechnet werden soll.

Grundrechnungen:

Addition	( x1+ jy1) + (x2+jy2) = (x1 + x2) + j(y1 + y2)
Subtraktion:	( x1+ jy1) – (x2+jy2) = (x1 – x2) + j(y1 – y2).
Multiplikation :	( x1+ jy1) * (x2+jy2) = (x1x2-y1y2) + j(x1y2 +x2y1). Die Beträge multiplizieren sich und die Phasen addieren sich (das Minuszeichen kommt aus dem j2 )
Division	als Betrag |z| ergibt sich von |z1/ |z2| die Phasen werden Subtrahiert
Betrag:
Phase:	ø = arctan ( y/x )
Real- und Imaginärteil	x = |z| * cos (ø). und y = |z| * sin(ø)