Phase Shift Keying (PSK) ist ein digitales Modulationsverfahren, bei dem die Phase eines Trägersignals verwendet wird, um digitale Daten zu übertragen. Bei PSK wird die Phase des Trägersignals je nach den zu übertragenden Daten verändert. Die Idee ist, dass verschiedene Phasenlagen des Signals bestimmten Datenwerten (Bitmustern) entsprechen, sodass die Information durch die Phasenänderungen kodiert wird.
Funktionsweise von PSK:
- Trägersignal: Das Trägersignal ist ein sinusförmiges Signal mit einer konstanten Frequenz.
- Phasenänderung: Das Trägersignal wird in unterschiedlichen Phasen moduliert, um digitale Informationen zu übertragen. Jede Änderung in der Phase repräsentiert ein Bit oder eine Gruppe von Bits.
Typen von PSK:
Es gibt verschiedene Formen von PSK, abhängig davon, wie viele Phasenunterschiede verwendet werden, um die Daten zu kodieren:
- BPSK (Binary Phase Shift Keying):
- Hier gibt es zwei Phasenzustände: 0° und 180°.
- Jedes Bit wird durch einen Phasenwechsel dargestellt:
- 0° repräsentiert z. B. ein Bit „0“.
- 180° repräsentiert z. B. ein Bit „1“.
- Es ist die einfachste Form von PSK, daher auch robust gegen Rauschen, aber die Datenrate ist begrenzt.
- QPSK (Quadrature Phase Shift Keying):
- Bei QPSK werden vier verschiedene Phasenzustände verwendet: 0°, 90°, 180°, und 270°.
- Da vier Phasen verwendet werden, können zwei Bits pro Phasenänderung übertragen werden (z. B. „00“, „01“, „10“, „11“).
- QPSK ermöglicht eine höhere Datenrate als BPSK bei gleicher Bandbreite.
- 8-PSK:
- Hier gibt es acht verschiedene Phasenzustände (z. B. 0°, 45°, 90°, 135°, 180°, 225°, 270°, 315°).
- Dadurch können drei Bits pro Symbol übertragen werden, was die Datenrate weiter erhöht.
- Mit mehr Phasenzuständen wird das System allerdings empfindlicher gegenüber Rauschen und Signalstörungen.
PSK am Beispiel von Numpy.
Im folgenden code wird ein PSK Signal erzeugt, das den ASCII Code übertragen soll.
Ein ASCII Zeichen wird dabei in 2 Teile zerlegt und jeweils mit 16Bit übertragen.
Bsp.: Das Zeichen “z” hat den HexCode 0x7A. Es wird also zunächst die 7 und anschließend das A übertragen.
Der Code für das PSK Signal ist folgender:
import numpy as np
import matplotlib.pyplot as plt
# Parameter
carrier_freq = 100e3 # 100 kHz Trägerfrequenz
sampling_rate = 1e6 # Abtastrate von 1 MHz
symbol_duration = 1e-3 # Dauer eines Symbols (1 ms)
message = "" # Textnachricht
for i in range(255):
message = message + chr(i)
# ASCII-Werte der Zeichen im Text
ascii_values = [ord(char) for char in message]
print(f"ASCII-Werte: {ascii_values}")
# Umwandlung von ASCII in 2 Symbole (je 4 Bits)
binary_message = []
for value in ascii_values:
binary_value = bin(value)[2:].zfill(8) # ASCII-Wert in 8-Bit Binär umwandeln
binary_message.extend([binary_value[:4], binary_value[4:]]) # In zwei 4-Bit-Symbole aufteilen
# Anzahl der Phasen für das PSK-Signal (32 Phasen für 5-Bit)
num_phases = 16
# Berechnung der Phasenverschiebung für jedes Symbol und Speicherung im Konstellationsdiagramm
constellation_points = []
for symbol in binary_message:
symbol_value = int(symbol, 2) # Binärsymbol in Zahl umwandeln
phase_shift = (2 * np.pi * symbol_value) / num_phases # Berechne die Phase basierend auf der Anzahl der Phasen
# Speichere den Punkt im komplexen Plan
real_part = np.cos(phase_shift) # Realteil (Amplitude entlang der x-Achse)
imag_part = np.sin(phase_shift) # Imaginärteil (Amplitude entlang der y-Achse)
constellation_points.append(complex(real_part, imag_part)) # Punkt als komplexe Zahl speichern
# Konstellationsdiagramm plotten
plt.figure(figsize=(8, 8))
for point in constellation_points:
plt.plot(point.real, point.imag, 'bo') # Plotte die Punkte im Diagramm
plt.title("Konstellationsdiagramm für PSK Signal (ohne Paritätsbit)")
plt.xlabel("Realteil (Amplitude entlang der x-Achse)")
plt.ylabel("Imaginärteil (Amplitude entlang der y-Achse)")
plt.grid(True)
plt.axis('equal') # Gleiche Skala für x und y Achse
plt.show()
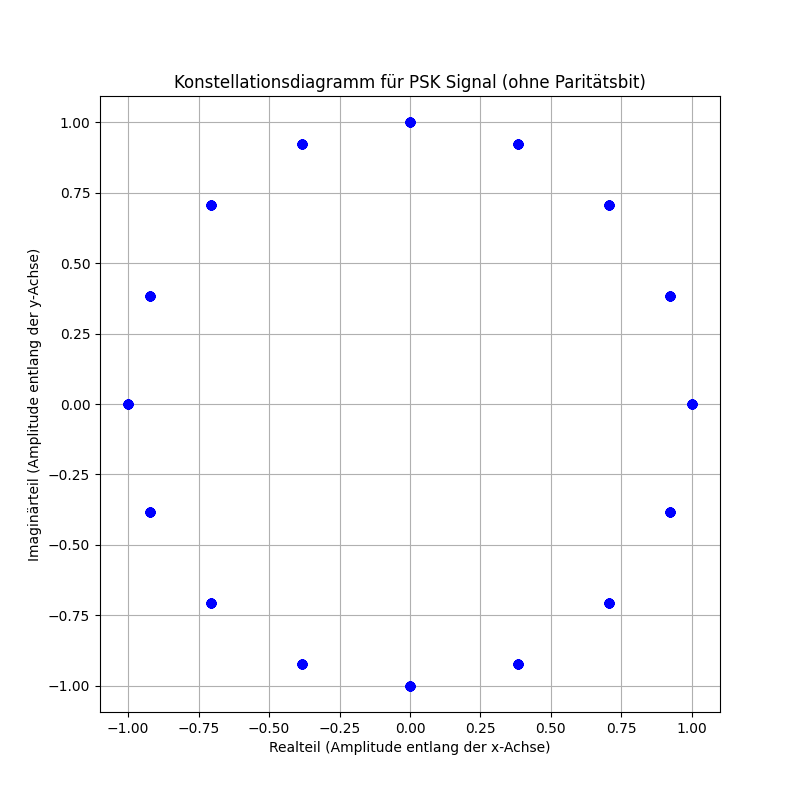
Code-Sprache: PHP (php)Im Constellation Diagramm ergibt sich dann folgendes Bild, wenn man alle Zeichen aus dem Code überträgt:
Demodulation
Für die Demodulation des Signals werden die einzelnen Phase im Signal wieder ermittelt.
Wir folgen dabei im Wesentlichen dem Prozess der hier beschrieben ist: Digitale Modulation
Das modulierte Signal besteht nun aus einer Folge von Symbolen, wobei jedes Symbol für eine feste Zeitdauer (symbol_duration) ein bestimmtes Bitmuster repräsentiert. Um die Phasen jedes Symbols zu analysieren, muss das Signal in Blöcke segmentiert werden, die der Länge eines Symbols entsprechen.
# Demodulationsfunktion
def demodulate_psk(psk_signal, carrier_freq, sampling_rate, symbol_duration, num_phases):
Args:
psk_signal (numpy.ndarray): Das modulierte PSK-Signal.
carrier_freq (float): Trägerfrequenz in Hz.
sampling_rate (float): Abtastrate in Hz.
symbol_duration (float): Dauer eines Symbols in Sekunden.
num_phases (int): Anzahl der möglichen Phasen (z. B. 32 für 5-Bit-PSK).
Returns:
list of str: Liste der Binärsymbole, die demoduliert wurden.
"""
samples_per_symbol = int(sampling_rate * symbol_duration)
phase_step = 2 * np.pi / num_phases # Schrittweite zwischen den Phasen
symbol_bins = np.arange(0, 2 * np.pi, phase_step) # Alle möglichen Phasen
demodulated_symbols = []
# Iteriere über das Signal in Blöcken mit der Länge eines Symbols
for i in range(0, len(psk_signal), samples_per_symbol):
# Extrahiere ein Symbol (entspricht der Dauer eines Symbols)
symbol_segment = psk_signal[i:i + samples_per_symbol]
if len(symbol_segment) < samples_per_symbol:
break # Letzter Block könnte kürzer sein
<mark style="background-color:rgba(0, 0, 0, 0)" class="has-inline-color has-vivid-cyan-blue-color"><strong># Rekonstruiere die Phase des Symbols
t = np.arange(len(symbol_segment)) / sampling_rate
reference_carrier = np.cos(2 * np.pi * carrier_freq * t) # Referenzträger
phase = np.angle(np.sum(symbol_segment * reference_carrier)) # Berechne die Phase
</strong></mark>
# Mappe die Phase auf das nächste Bin
phase = (phase + 2 * np.pi) % (2 * np.pi) # Stelle sicher, dass Phase positiv ist
closest_bin = np.argmin(np.abs(symbol_bins - phase)) # Finde die nächste gültige Phase
# Speichere das Symbol (Binärwert des Phasenindex)
demodulated_symbols.append(format(closest_bin, f'0{int(np.log2(num_phases))}b'))
return demodulated_symbols
Code-Sprache: PHP (php)Die Multiplikation des modulierten Signals (symbol_segment) mit dem Referenzträger (reference_carrier) hebt die Phase des Symbols hervor. Mathematisch entspricht dies einer Mischung des Signals, wobei die Phase des Symbols relativ zum Träger sichtbar wird. Der Träger ist also das Referenzsignal zur bestimmung der Phase.
Formel : y(t)=s(t)⋅cos(2πfct).
Nach der Multiplikation bleiben nur die niederfrequenten Anteile übrig, die Informationen über die Phase des Symbols tragen.
Es ergibt sich ein Signal mit schwankender Amplitude und Phase. Um eine stabile Phase für das gesamte Symbol zu bestimmen wird durch die Summierung wird das Signalrauschen reduziert und die Phaseninformation verstärkt.
Nach der Summierung liegt ein komplexer Wert vor (Summe von sinus- und kosinusmodulierten Anteilen). Die Phase kann mit der Funktion np.angle() aus dem komplexen Signal berechnet werden.
Da die erhaltenen Phasenwerte in einem Kreis von 0 bis 2π liegen, muss die Phase normalisiert werden, um sicherzustellen, dass sie in diesem Bereich bleibt. Zusätzlich muss sie auf den nächstgelegenen Konstellationspunkt im PSK-Konstellationsdiagramm gemappt werden.
Der nächstgelegene Konstellationspunkt repräsentiert ein spezifisches Binärsymbol.
Die so erhaltenen Binärwerte können wieder zu einer zusammenhängenden Binärfolge zusammengefügt werden. Daraus lässt sich die ursprüngliche Nachricht ermitteln.
Bei der Demodulation eines PSK-Signals müssen Sie wissen, wo der Beginn jedes Zeichens liegt, um das Signal korrekt in Symbole zu segmentieren.
Das obige Programm berücksichtigt dies noch nicht. Eine Demodulation ist hier nur möglich, weil wir den Beginn des Zeichens aus dem generierten Signal sicher kennen.
In echten Signalen muss der Beginn eines Symbols zunächst erkannt werden.
Für die Symbolerkennung können verschiedene Verfahren zum Einsatz kommen:
- Verwendung eines Präambels (Synchronisationssignal)
Der Sender fügt zu Beginn der Übertragung eine festgelegte Folge von Symbolen ein, die als Präambel dient. Die Präambel hat eine bekannte Phase oder Amplitudenfolge, die der Empfänger verwendet, um den Beginn der Übertragung zu erkennen.
Eine solche Präambel wird z.B. bei der Übertragung von Bildern oft verwendet. Jede neue Zeile eines Bildes wird dann z.B. mit einer 0 / 1 Folge eingeleitet.
Bei Bildern verliert man dadurch maximal eine Zeile, bis das Signal demoduliert werden kann. Eine laufenden Textübertragung kann man so nicht demodulieren, wenn die Präambel am Anfang des gesamten Textes ist.
Die Präambel kann mathematisch wieder durch Korrelation im Signal erkannt werden. - Frame-Synchronisation durch zusätzliche Marker
Wenn jedes Zeichen aus mehreren Symbolen besteht, kann ein spezieller Marker zwischen Zeichen hinzugefügt werden. Dieser Marker hat eine eindeutige Phase oder Amplitude, die nicht in den normalen Symbolen vorkommt.
Der Marker kann dann durch eine Mustererkennung gefunden werden. - Pilot-Symbol-Tracking
In längeren Übertragungen können regelmäßig eingefügte Pilot-Symbole verwendet werden, die synchron bleiben. Diese Pilot-Symbole haben eine spezifische, bekannte Phase oder Amplitude.
Der Empfänger synchronisiert sich durch Erkennung der Pilot-Symbole
Beispiel für die Verwendung eines Pilotsignals - Fehlerkorrektur und Selbstsynchronisation
Einige Übertragungsprotokolle verwenden redundante Daten oder Fehlerkorrekturcodes, um den Beginn eines Zeichens zu erkennen. Bei der Demodulation wird überprüft, ob die empfangenen Daten den erwarteten Mustern entsprechen, und die Synchronisation wird automatisch angepasst.
Beispiel: Ein 8-Bit-Zeichen wird durch ein Parity-Bit ergänzt, und nur gültige Binärmuster werden als Beginn eines Zeichens akzeptiert: