Wie auf der vorherigen Seite beschrieben, ist es bei der Demodulation von PSK erforderlich, den Beginn des jeweiligen Symbols korrekt zu ermitteln. Dazu kann man eine Pilotsequenz in as Signal einfügen.
Das folgende Beispiel zeigt den Einsatz eines Pilotsignals bei der Modulation und Demodulation.
Modulation des PSK Signals
Das folgende Programm generiert die Sampling Werte für ein solches Pilotsignal. Es wird vor dem eigentlichen Signal ausgesendet. Wie beim Signal selbst, wird jedes ASCII Zeichen in Form von 2 Halbbytes dargestellt, damit die Übertragung mit PSK16 möglich ist.
def generate_pilot_signal(pilot_text, carrier_frequency, sampling_rate, symbol_duration):
"""Generiert und speichert das modulierte Signal des Pilotsymbols."""
# ASCII-Zeichen in Symbole (4-Bit pro Symbol) kodieren
symbols = []
for char in pilot_text:
ascii_value = ord(char)
high_nibble = (ascii_value >> 4) & 0xF # Höhere 4 Bits
low_nibble = ascii_value & 0xF # Niedrigere 4 Bits
symbols.extend([high_nibble, low_nibble])
# Träger-Signalparameter
samples_per_symbol = int(sampling_rate * symbol_duration)
t = np.linspace(0, symbol_duration, samples_per_symbol, endpoint=False)
# Modulation
pilot_signal = []
for symbol in symbols:
phase = (symbol / 15) * 2 * np.pi
carrier = np.cos(2 * np.pi * carrier_frequency * t + phase)
pilot_signal.extend(carrier)
# Rückgabe des Pilotsignals als numpy-Array
return np.array(pilot_signal)
# Additives Weißes Gaußsches Rauschen (AWGN)
def add_awgn_noise(signal, snr_db):
"""Fügt Additives Weißes Gaußsches Rauschen (AWGN) zu einem Signal hinzu."""
signal_power = np.mean(np.abs(signal)**2)
snr_linear = 10**(snr_db / 10)
noise_power = signal_power / snr_linear
noise = np.sqrt(noise_power) * np.random.randn(len(signal))
return signal + noise
# Kanalverzerrung (FIR-Filter):
def simulate_channel(signal, channel_response):
"""Simuliert eine Kanalverzerrung (z. B. FIR-Filter)."""
# Erhalte Signal gleicher Länge wie das Original
return np.convolve(signal, channel_response, mode='full')[:len(signal)]Der gewünschte Text wird in folgender Funktion moduliert. Um ein möglichst realistisches Signal zu erhalten wird zudem Rauschen hinzugefügt. Weiterhin soll simuliert werden, dass vor dem Start der Übertragung nur Rauschen vorhanden ist.
def modulate_psk_with_pilot(
text,
pilot_text,
carrier_frequency,
sampling_rate,
symbol_duration,
snr_db
):
# Generiere das Pilotsignal
pilot_signal = generate_pilot_signal(
pilot_text, carrier_frequency, sampling_rate, symbol_duration
)
# ASCII-Zeichen in Symbole (4-Bit pro Symbol) kodieren
symbols = []
for char in text:
ascii_value = ord(char)
high_nibble = (ascii_value >> 4) & 0xF # Höhere 4 Bits
low_nibble = ascii_value & 0xF # Niedrigere 4 Bits
symbols.extend([high_nibble, low_nibble])
# Träger-Signalparameter
samples_per_symbol = int(sampling_rate * symbol_duration)
t = np.linspace(0, symbol_duration, samples_per_symbol, endpoint=False)
# Modulation des Hauptsignals
main_signal = []
for symbol in symbols:
phase = (symbol / 16) * 2 * np.pi
carrier = np.cos(2 * np.pi * carrier_frequency * t + phase)
main_signal.extend(carrier)
# Zufälliges Rauschen vor dem Sihnal
dummy = np.random.uniform(0, 0, 500)
# Gesamtsignal ohne Rauschen
full_signal = np.concatenate([dummy, pilot_signal, main_signal])
# Simuliere Kanalverzerrungen, falls angegeben
if channel_response is not None:
signal = simulate_channel(full_signal, channel_response)
# Füge Rauschen hinzu
signal_with_noise = add_awgn_noise(signal, snr_db)
return signal_with_noise, pilot_signalDas Ergebnis sieht dann wie folgt aus:
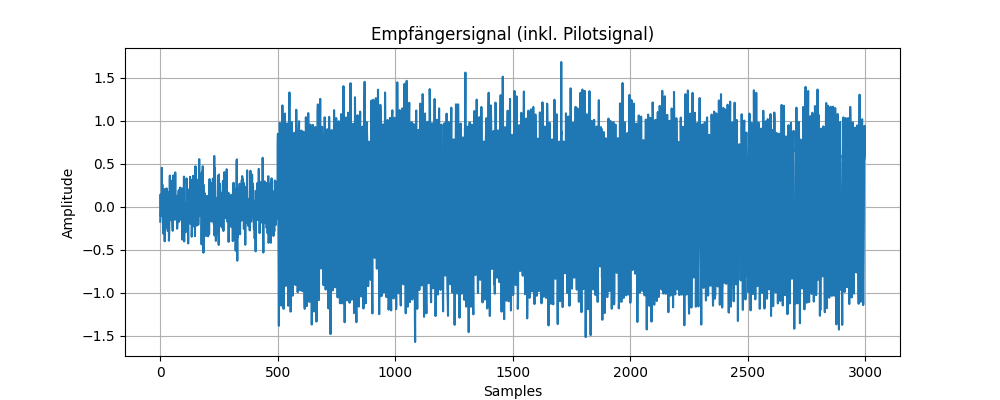
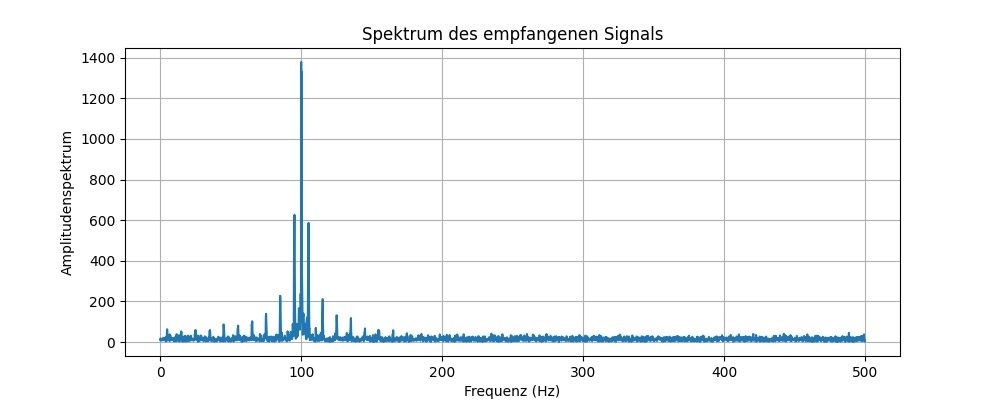
Demodulation des Signals
Im ersten Schritt. wird die Position des Pilotsignals ermittelt. Dies geschieht mittels Korrelation. Das verwendete Prinzip ist hier genauer beschrieben
Diese Funktion bestimmt den Start des Pilotsignals im empfangenen Signal. Durch die Verwendung der Korrelation kann das Signal auch im Rauschen erkannt werden.
def normalized_cross_correlation(sample, muster):
muster_norm = np.linalg.norm(muster)
correlation = []
for i in range(len(sample) - len(muster) + 1):
ausschnitt = sample[i:i + len(muster)]
ausschnitt_norm = np.linalg.norm(ausschnitt)
if ausschnitt_norm == 0 or muster_norm == 0: # Division durch Null vermeiden
correlation.append(0)
else:
korr = np.dot(ausschnitt, muster) / (ausschnitt_norm * muster_norm)
correlation.append(korr)
return np.array(correlation)
Das empfangene Signal wird nun nach dem Pilotsignal wieder in seine Ursprungszeichen zurück konvertiert
def demodulate_psk_with_pilot(signal, carrier_frequency, sampling_rate, symbol_duration, start_index):
# Parameter berechnen
samples_per_symbol = int(sampling_rate * symbol_duration)
t = np.arange(samples_per_symbol) / sampling_rate
reference_carrier = np.exp(-1j * 2 * np.pi * carrier_frequency * t)
# Symbole demodulieren
demodulated_symbols = []
for i in range(start_index, len(signal), samples_per_symbol):
symbol_segment = signal[i:i + samples_per_symbol]
if len(symbol_segment) < samples_per_symbol:
break
# Multiplikation mit Referenzträger
mixed_signal = symbol_segment * reference_carrier
# Summieren und Phase extrahieren
phase = np.angle(np.sum(mixed_signal))
# Bestimmen des Symbols aus der Phase
symbol_index = int(np.round((phase / (2 * np.pi)) * 16)) % 16
demodulated_symbols.append(symbol_index)
# Symbole in Text umwandeln
text = ""
for i in range(0, len(demodulated_symbols), 2):
if i + 1 >= len(demodulated_symbols):
raise ValueError("Unvollständiges Symbolpaar erkannt.")
high_nibble = demodulated_symbols[i]
low_nibble = demodulated_symbols[i + 1]
ascii_value = (high_nibble << 4) | low_nibble
text += chr(ascii_value)
return textAufruf des Programms und Ergebnis:
import numpy as np
import matplotlib.pyplot as plt
... Funktionen
# Parameter
text = "ABCDEFGHIJKLMNOPQRTSUVW". # zu übertragender Text
pilot_text = chr(0xFF) + chr(0xFF) # Pilotsymbol: 3 Zeichen
carrier_frequency = 100 # Hz
sampling_rate = 1000 # Hz
symbol_duration = 0.1 # Sekunden pro Symbol
snr_db = 10 # SNR in Dezibel
channel_response = [1, -0.3, 0.1] # Ein einfaches Kanalmodell (FIR-Filter)
# Modulation
received_signal, pilot_signal = modulate_psk_with_pilot(
text, pilot_text, carrier_frequency, sampling_rate, symbol_duration, snr_db
)
# Position des Pilotsignals bestimmen
cor = normalized_cross_correlation(received_signal, pilot_signal)
maxpos = np.argmax(cor)
print("Start Pilotsignal", maxpos)
# Demodulation nach dem Pilotsignal
demod = demodulate_psk_with_pilot(received_signal, carrier_frequency, sampling_rate, symbol_duration,maxpos+len(pilot_signal))Ergebnis:
Start Pilotsignal 500
Länge des Pilotsignals: 400
Länge des gesamten Signals: 5500
ABCDEFGHIJKLMNOPQRTSUVWDurch das hinzufügen von zusätzlichem Rauschen tritt irgendwann der Effekt ein, dass die Zeichen nicht mehr korrekt erkannt werden können.
Das Signal ist dann stark verzerrt:
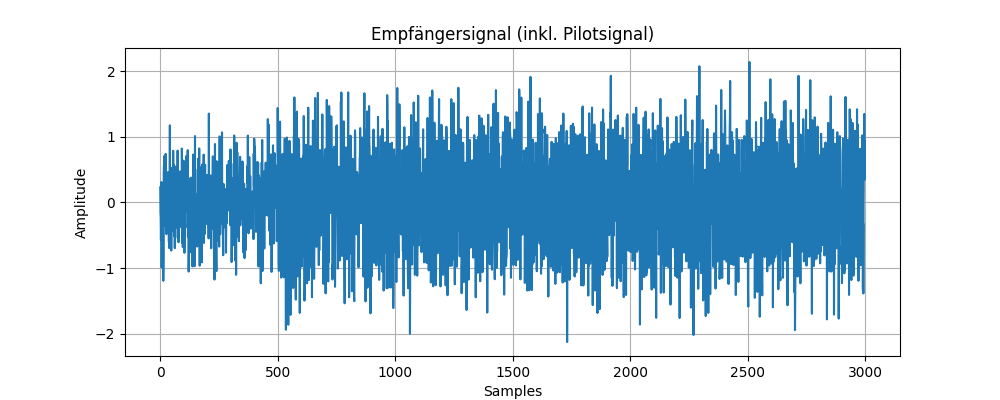
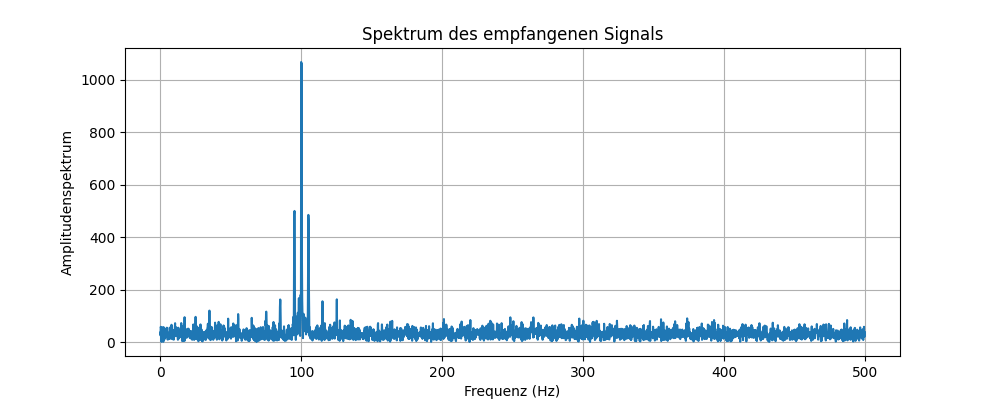
Bei SNR = 1 wird das Pilotsignal noch erkannt, die einzelnen Zeichen enthalten jedoch Fehler: ABCEEFHHIJ[L]OOPRReSeVW
Eine weitere Optimierung der Übertragung kann nun noch durch den Einsatz fehlerkorrigierende Codes erreicht werden.