Die Fourier-Transformation ist eine mathematische Methode, die eine Funktion der Zeit in ihre Frequenzkomponenten zerlegt.
Die Fourier-Transformation stellt ein periodisches Signal als Summe von einzelnen Sinuswellen verschiedener Frequenzen dar.
Jede der einzelnen Sinus Funktionen hat dabei eine bestimmte Amplitude und Phase bezogen auf ein Referenzsignal (z.B. dem lokalen Oszillator) und eine Periodendauer bzw. Frequenz.
Im folgenden Beispiel stellen wir uns vor, dass ein Rechteck-Signal mittels der Fouriertransformation abgebildet werden soll. Die Addition der folgenden 5 Signale gibt schon einen guten Eindruck vom Endergebnis.
y= 3sin(x)+sin(3x)+0.8sin(5x)+0.4sin(7x)+0.2sin(9x ) …
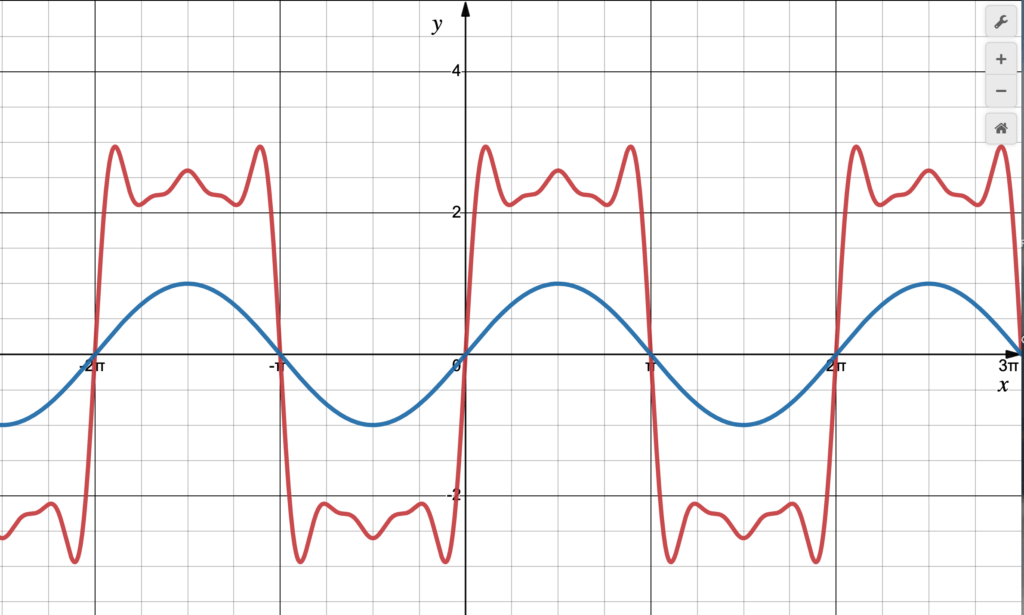
Nimmt man an, dass jeder Abschnitt auf der x-Achse 1ms dauert, dann kann man sehen, dass eine Schwingung 8ms benötigt, bis sie sich wiederholt. Dieser Wert heißt Periodendauer. Die Frequenz ist der Kehrwert der Periodendauer also 1/8ms = 125Hz.
In blau ist die Grundfrequenz abgebildet, summiert werden dazu noch ungerade Vielfache dieser Frequenz. Die dreifache Frequenz ist demnach 375Hz, die fünffache 625Hz etc.
Es ist damit gut vorstellbar, dass sich jede Frequenz eines der Sinussignale mit seiner Amplitude im Spektrum wiederfindet.
Um ein Signal perfekt abzubilden, wird eine unendliche Anzahl an Sinuswellen benötigt.
Allgemein wird die Fourier-Transformation daher als Integral mit folgender Gleichung definiert:
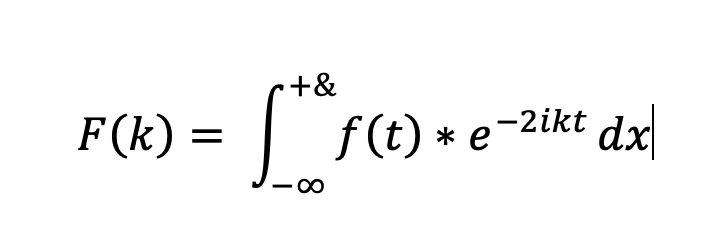
Die Exponentialfunktion enthält hierbei die sin und cos Anteile. Das Integral summiert eine unendliche Anzahl der sin und cos Wellen, um das originale Signal in dessen Spektrum korrekt abzubilden. Umgekehrt kann auch aus dem Frequenzbereich über die inverse Fourier Transformation das Signal im Zeitbereich errechnet werden.
Glücklicherweise müssen wir uns in der diskreten Welt nicht mit Integralen beschäftigen.
Die Diskrete Fourier-Transformation (DFT) ist eine Variante der Fourier-Transformation, die speziell für die Verarbeitung diskreter oder abgetasteter Signale entwickelt wurde. Während die Fourier-Transformation mit kontinuierlichen, periodischen Funktionen arbeitet, wird die DFT verwendet, um die Frequenzkomponenten einer diskreten Folge von Datenpunkten zu analysieren.
Eine definierte Anzahl an Datenpunkten wird hierbei als Basis in die Berechnung einbezogen. Diese Anzahl muss z.B. im gnuradio-companion entsprechend ausgewählt werden. Die FFT-Größe ist in der Regel eine Potenz von 2, um eine effiziente Berechnung zu ermöglichen, z. B. 32, 64, 128 usw.
Die Fourier-Transformation hat ein breites Anwendungsspektrum, z. B. die Analyse und Manipulation von Signalen, die Lösung von Differentialgleichungen, die Bildverarbeitung, die Datenkompression und die Audioverarbeitung. Sie ist ein leistungsfähiges Werkzeug zum Verständnis des Frequenzinhalts eines bestimmten Signals oder einer Funktion.
Die FFT-Größe wirkt sich auf die Frequenzauflösung und die Berechnungskomplexität der DFT aus. Eine größere FFT-Größe bietet eine bessere Frequenzauflösung, d. h. sie kann zwischen eng beieinander liegenden Frequenzen genauer unterscheiden. Allerdings erfordert sie auch mehr Rechenressourcen und Verarbeitungszeit.
Die Beziehung zwischen der FFT-Größe und der Frequenzauflösung wird durch die Abtastrate des Eingangssignals bestimmt. Die Frequenzauflösung kann mit der folgenden Formel berechnet werden:
Frequenzauflösung = (Abtastrate) / (FFT-Größe)
Bei einer FFT-Größe von 8192 und einer Abtastrate von 100kHz beträgt die Frequenzauflösung beispielsweise etwa 12,2 Hz.
Zur effizienten Berechnung der DFT und IDFT wurden schnelle Algorithmen wie die Fast Fourier Transform (FFT) entwickelt.
Im gnuradio-companion kann mit Hilfe der FFT das Spektrum eines Signals leicht dargestellt werden