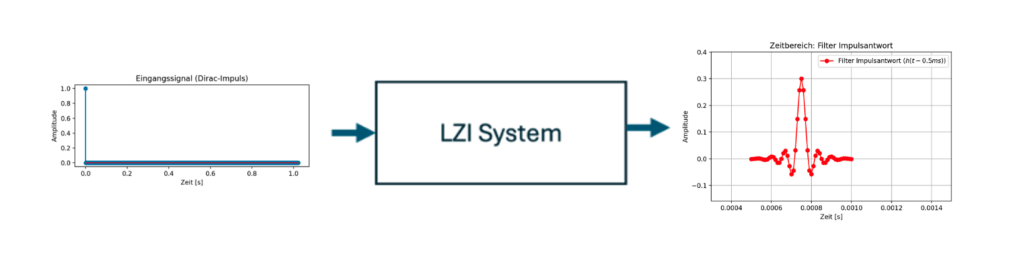
Ein lineares, zeitinvariantes (LZI) System ist eine grundlegende Kategorie von Systemen in der Signalverarbeitung, die sich durch zwei wesentliche Eigenschaften auszeichnet: Linearität und Zeitinvarianz.
Die Linearität eines Systems bedeutet, dass es das Superpositionsprinzip erfüllt. Dies beinhaltet, dass die Reaktion des Systems auf eine Summe von Eingangssignalen gleich der Summe der Reaktionen auf jedes einzelne Eingangssignal ist.
Mathematisch ausgedrückt bedeutet dies, dass für ein System mit einer Funktion f, die einen Eingang x auf einen Ausgang abbildet, gilt: f(x) + f(y) = f(x + y).
Darüber hinaus beinhaltet die Linearität auch das Homogenitätsprinzip, welches besagt, dass eine Skalierung des Eingangssignals um einen Faktor zu einer identischen Skalierung des Ausgangssignals führt. Die mathematische Definition eines linearen Systems fasst diese beiden Prinzipien zusammen als:
L(αx1(t) + βx2(t)) = αL(x1(t)) + βL(x2(t)),
wobei α und β Konstanten sind.
Die zweite Eigenschaft eines LZI Systems ist die Zeitinvarianz. Ein System ist zeitinvariant, wenn eine Zeitverschiebung im Eingangssignal zu einer identischen Zeitverschiebung im Ausgangssignal führt. Anders ausgedrückt bedeutet dies, dass die Reaktion des Systems unabhängig vom Zeitpunkt der Anwendung des Eingangssignals ist. Wenn ein Eingangssignal x(t) die Ausgabe f(t) erzeugt, dann erzeugt ein zeitverschobenes Eingangssignal x(t – T) die entsprechend zeitverschobene Ausgabe f(t – T). Viele physikalische Systeme weisen diese Eigenschaften entweder exakt oder in guter Näherung auf.
Impulsantwort
Legt man an den Eingang eines LZI Systems einen Impuls, dann kann man die Impulsantwort messen. Die Impulsantwort charakterisiert ein LZI System vollständig. Das ist recht praktisch, da man durch die geeignete Auswahl von Funktionen die Impulsantworten und damit auch deren Einfluss auf das Eingangssignal bestimmen kann.
Für ein kontinuierliches System ist der Impuls mathematisch durch die Dirac Delta Funktion bestimmt. Ein unendlich kurzer Peak mit einer unendlichen Amplitude.
Für die Verwendung in der diskreten Welt ist das natürlich nicht sinnvoll.
Hier kommt die Kronecker-Delta-Funktion zum Einsatz. Über n Samples hinweg ist ergibt diese Funktion für n=0 den Wert 1 und für n<>0 den Wert 0.
Digitale Filter, sowohl FIR (Finite Impulse Response) als auch IIR (Infinite Impulse Response), sind Beispiele für LZI-Systeme und können in GNU Radio Companion einfach mithilfe der entsprechenden Filterblöcke wie “FIR Filter” und “IIR Filter” implementiert werden.
Die Konfiguration dieser Blöcke hängt von den gewünschten Eigenschaften des Filters ab. Die Filterkoeffizienten (auch Taps genannt) definieren direkt die Impulsantwort des FIR-Filters. Das folgende Beispiel beschreibt die Implementierung eines Filters und die Ermittlung der Koeffizienten genauer.
Die Impulsantwort des Blocks kann man mit einem approximativen Impuls am Eingang des Filterblocks erzeugen und die die Impulsantwort des Filters am Ausgang beobachten. Einen solchen Impuls kann man z.B. mit der Signal Source, Waveform fixed, frequency = 0Hz nd 1 sample mit repeat = no.
Implementierung am Beispiel eines FIR Tiefpass Filters
Ein FIR-Filter (Filter mit endlicher Impulsresponse) ist ein Digitalfilter, dessen Impulsantwort eine endliche Länge hat. Die Ausgabe eines FIR-Filters wird ausschließlich als gewichtete Summe der aktuellen und einer endlichen Anzahl vergangener Eingangssamples berechnet. Die Filterkoeffizienten sind dabei die Gewichtungen dieser Eingangssamples.
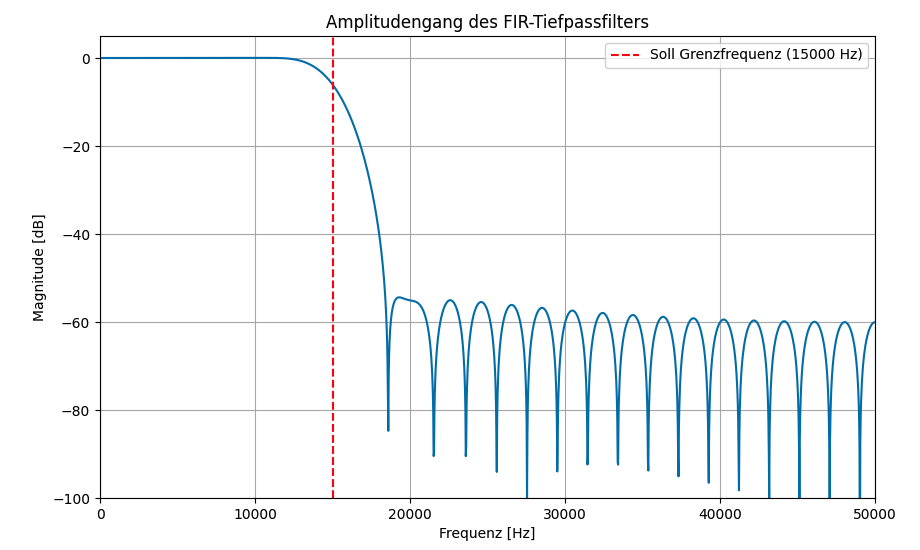
Die Impulsantwort des FIR-Filters (also die Folge seiner Koeffizienten) ist das Ergebnis der Multiplikation (im Zeitbereich) der abgetasteten idealen Impulsantwort (z.B. basierend auf der Sinc-Funktion für einen Tiefpass) mit der abgetasteten Fensterfunktion (wie dem Hamming-Fenster). Die Fensterfunktion bei der FIR-Filterauslegung wird verwendet, um die Welligkeit im Frequenzgang insbesondere im Sperrbereich zu reduzieren, die ansonsten durch das einfache, abrupte Abschneiden der idealen Impulsantwort entstehen würde.
Beispiel eines Tiefpassfilters:
Abtastrate (fs): 100kHz
Frequenz des Signals: 10kHz
Gewünschte Grenzfrequenz (fc): 15k Hz
Nyquist-Frequenz: 50000.0 Hz. (Hälfte der Abtastrate)
Normalisierte Grenzfrequenz: 0.3. (Grenzfrequenz / Nyquistfrequenz)
Filterlänge bzw. Anzahl der Koeffizienten (N): 51
Fensterfunktion: Hamming
Berechnung der Koeffizienten
fir_coeffs = signal.firwin(N, fc_normalized, window='hamming')
Berechnung des Frequenzgangs
w, h = signal.freqz(fir_coeffs, [1.0], worN=2000)
w enthält nun die Frequenzpunkte, an denen der Frequenzgang berechnet wurde. Diese Werte liegen typischerweise im Bereich von 0 bis π Radiant pro Sample.
h enthält die komplexen Frequenzgangwerte an den entsprechenden Frequenzpunkten in w. Jedes Element in h ist eine komplexe Zahl. Der Betrag dieser komplexen Zahl (|h|) gibt die Verstärkung (Magnitude) des Filters bei dieser Frequenz an (hier in dB, 20⋅log10(∣h∣)). Der Winkel dieser komplexen Zahl (∠h) gibt die Phasenverschiebung an.
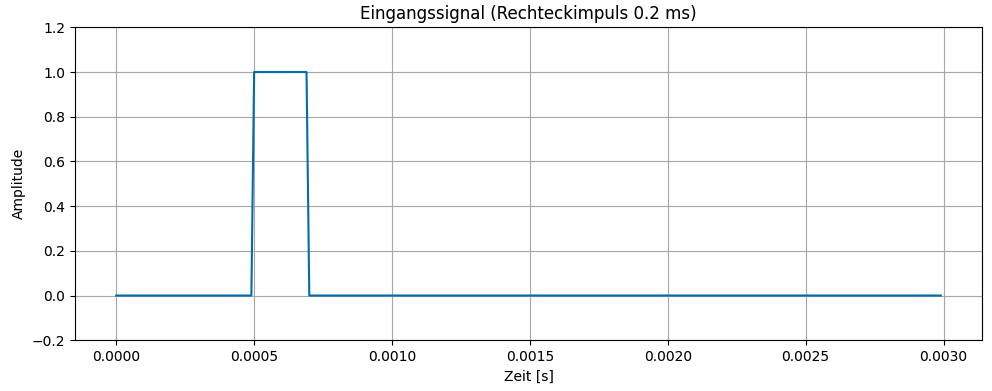
Legt man nun an den Eingang des Filters einen kurzen Rechteck Impuls, so kann das Ausgangssignal berechnet werden.
Im folgenden Code wird der Eingangsimpuls als ein Python Array mit Samplewerten berechnet und mit der Impulsantwort (Liste der Filter Koeffizienten) über die Faltung zum Ausgangssignal verknüpft.
# Erzeugen und Filtern des Eingangs-Impulssignals
pulse_duration_ms = 0.2
pulse_duration_samples = int(pulse_duration_ms * 1e-3 * fs) # Dauer in Samples
# Gesamtlänge des Testsignals: Länger als Impuls + Filterlänge, damit Reaktion abklingt
signal_length_samples = 300
input_signal = np.zeros(signal_length_samples)
# Platzieren des Impulses, z.B. beginnend bei Index 50
pulse_start_index = 50
input_signal[pulse_start_index : pulse_start_index + pulse_duration_samples] = 1.0
# Zeitachse für das Signal erstellen
t_signal = np.arange(signal_length_samples) / fs # Zeit in Sekunden
# Filter das Eingangssignal
filtered_signal = signal.lfilter(fir_coeffs, [1.0], input_signal)Das Ergebnis ist folgendes Signal im Zeitbereich
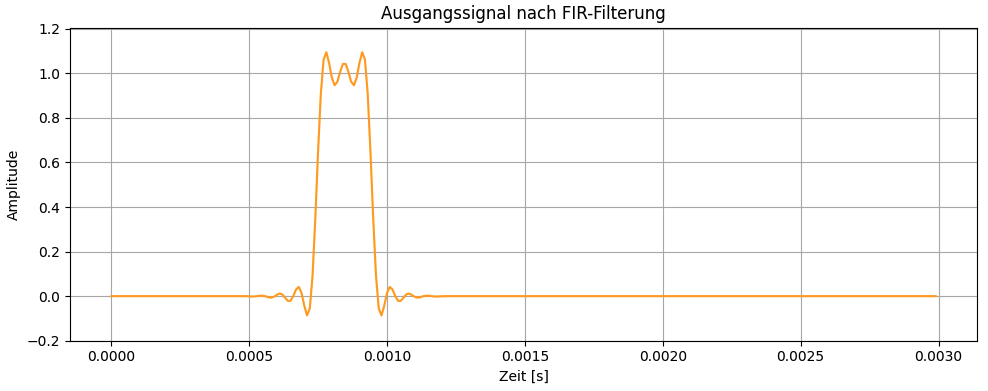
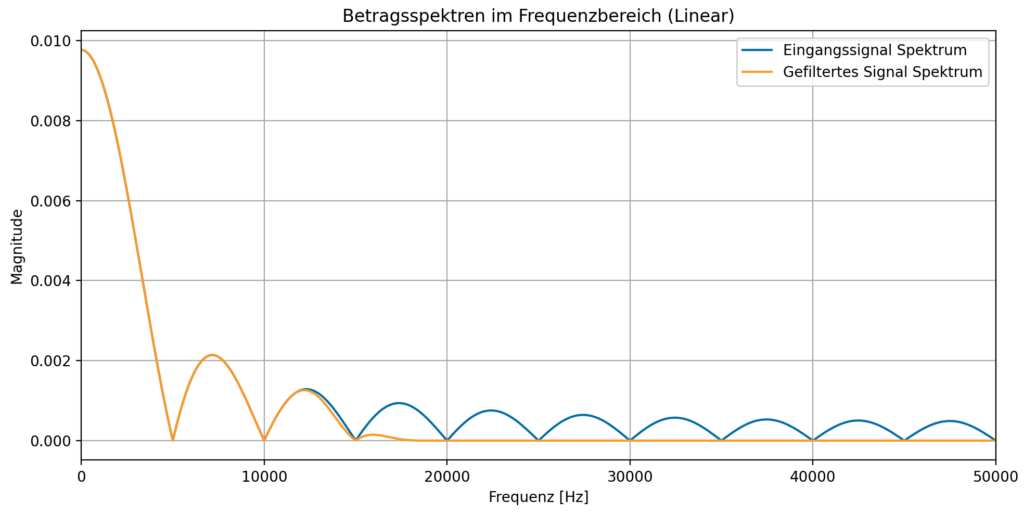
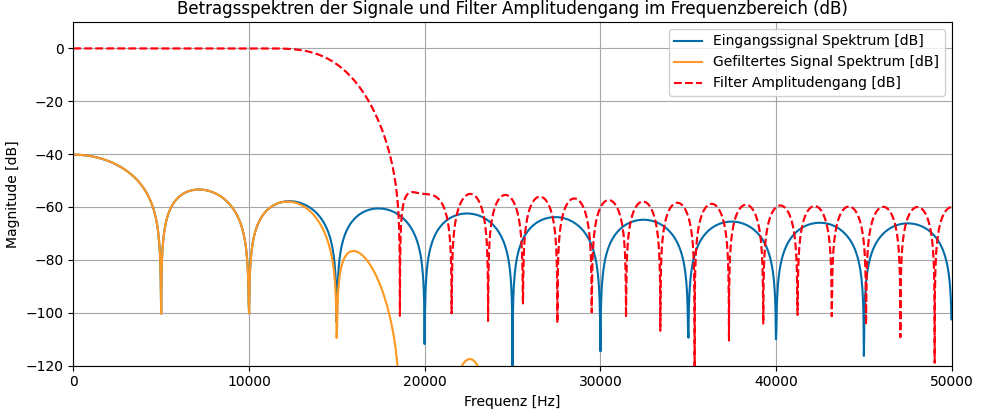
In der Darstellung im Frequenzbereich erkennt man, dass fir Frequenzanteile des gefilterten Signals ab der Grenzfrequenz von 15kHz deutlich abnehmen.
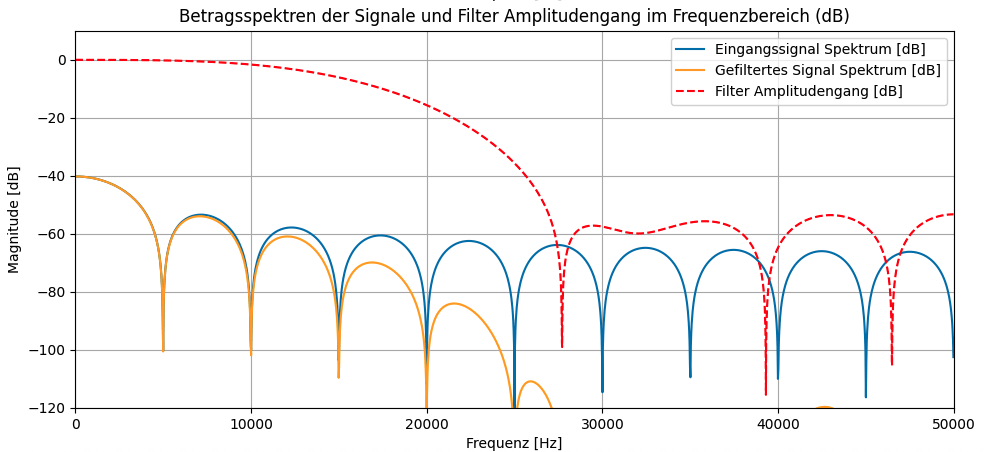
Reduziert man die Anzahl der Koeffizienten des Filters, so nimmt die Welligkeit zu. Der Filter ist weniger selektiv und mehr Frequenzanteile oberhalb der Grenzfrequenz sind im gefilterten Signal enthalten:
