in SDR ist die Verwendung linearer zeitinvarianter Systeme (LZI-Systeme) von zentraler Bedeutung, weil diese Systeme eine mathematisch handhabbare und effiziente Grundlage für die Signalverarbeitung bieten.
LZI-Systeme lassen sich durch Faltung und Frequenzanalyse (Fourier-Transformation) leicht analysieren. Die Eigenschaften der LZI-Systemen erleichtern die Berechnung der Systemantworten auf beliebige Eingangssignale, was die Implementierung von Modulation, Filterung und anderen Signalverarbeitungsoperationen stark vereinfacht.
Ein LZI-System kann vollständig durch die Reaktion auf einen Dirac-Impuls beschrieben werden. Das entstehende Ausgangssignal wird als Impulsantwort bezeichnet.
Die Impulsantwort gibt Auskunft darüber, wie das System auf jegliche Eingangsgrößen reagiert. Für jedes beliebige Eingangssignal kann der Ausgang dann durch die Faltung dieses Eingangssignals mit der Impulsantwort bestimmt werden. Diese Beschreibung ist zentral in der Systemtheorie und Signalverarbeitung und ermöglicht es, das Verhalten von LZI-Systemen sehr effizient zu analysieren und zu berechnen.
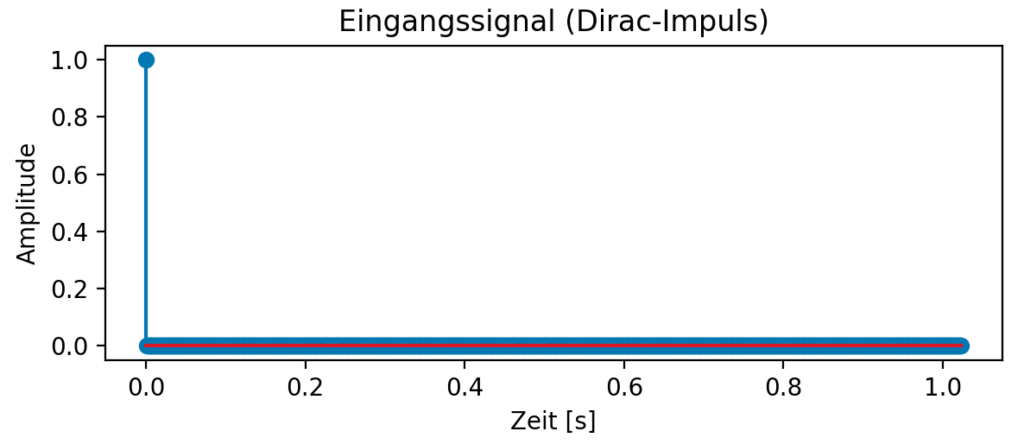
Der Dirac-Impuls (auch Dirac-Delta-Funktion genannt), ist ein idealisierter mathematischer Impuls. In der diskreten Zeit hat der Dirac-Impuls nur an einer Stelle den Wert 1 und für alle anderen den Wert 0.

Beispiel für einen Dirac Impuls
Eingangssignal
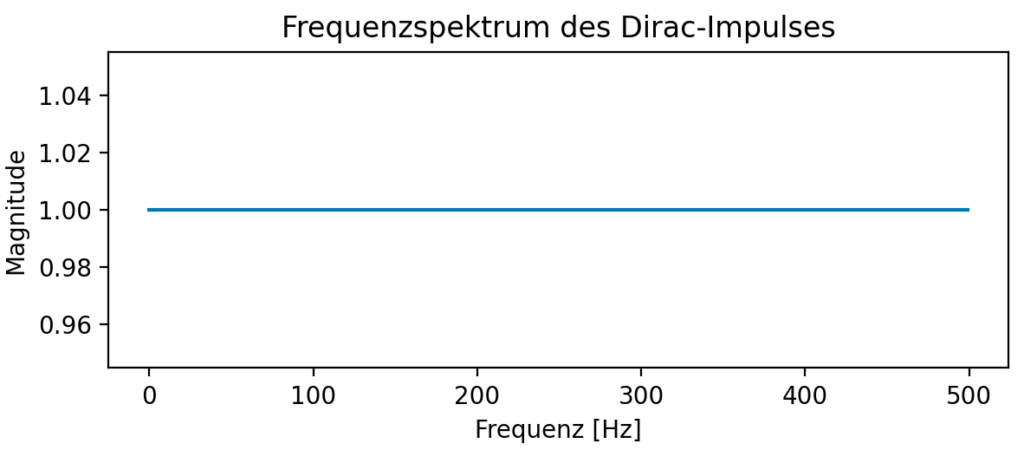
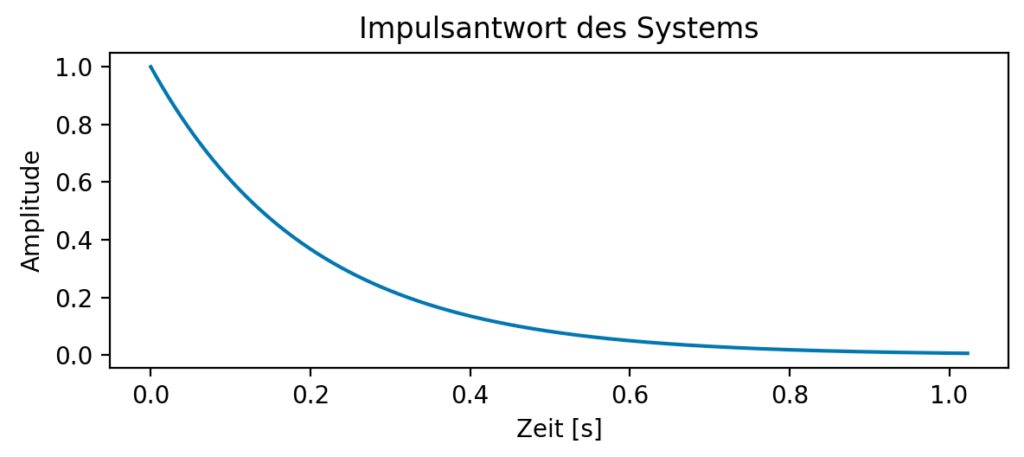
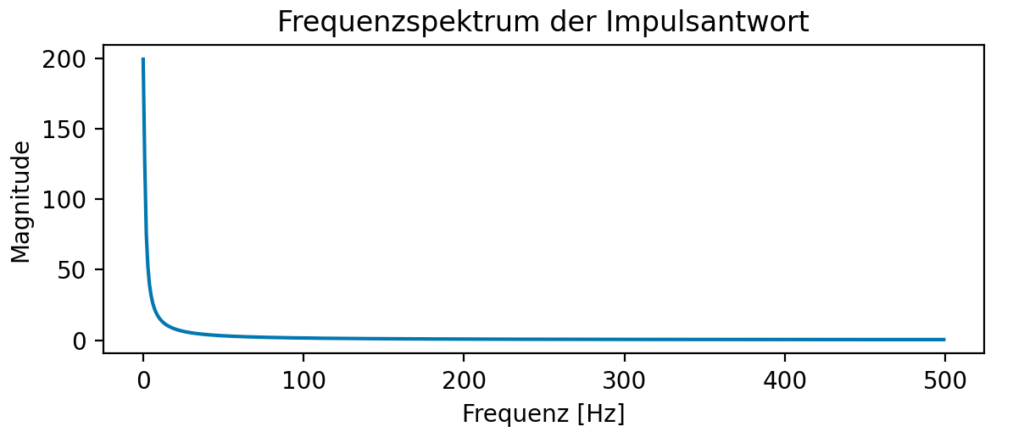
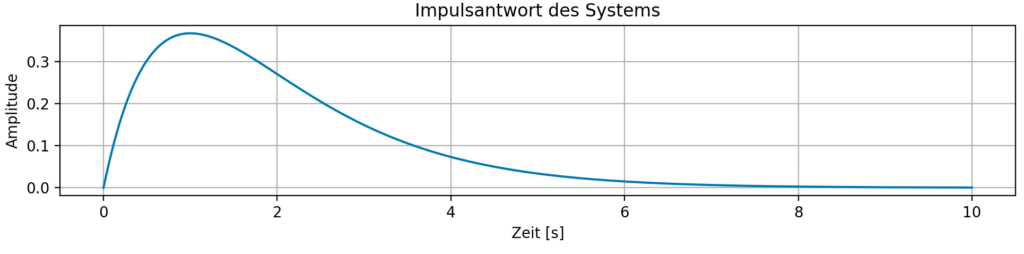
Impulsantwort
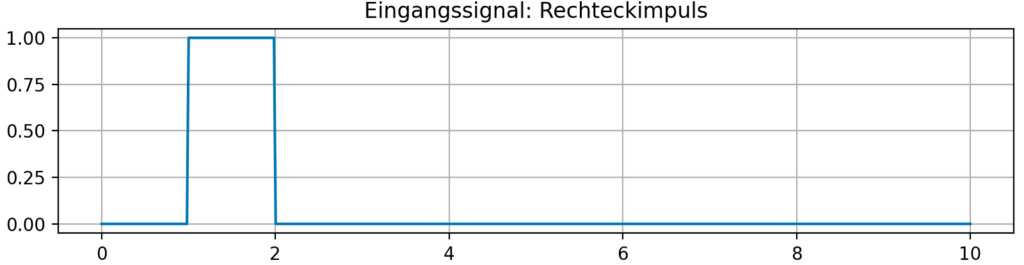
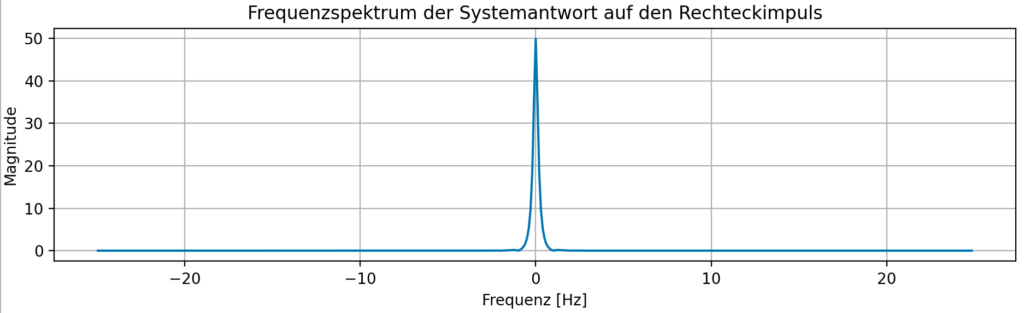
Beispiel für einen Rechteck Impuls
Eingangssignal
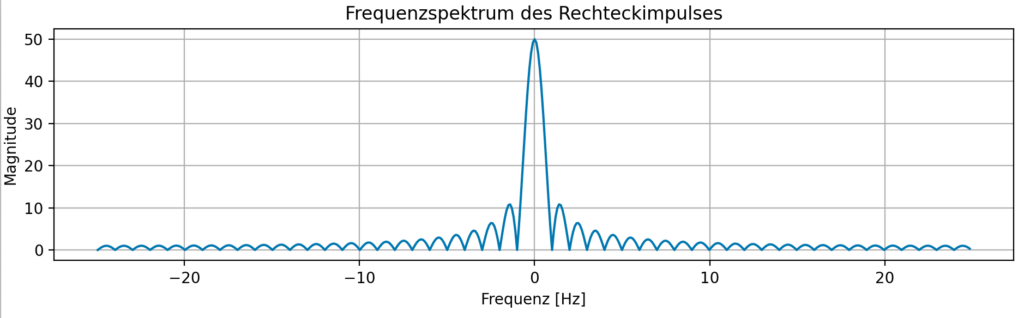
Impulsantwort
Filter als LZI System
Mit Hilfe der Eigenschaften von LZI Systemen lassen sich Filter für SDR realisieren.
Die Filterung eines Signals durch ein lineares zeitinvariantes (LZI) System wird im Zeitbereich durch die Faltung des Eingangssignals mit der Impulsantwort des Filters beschrieben. Die Impulsantwort h(t) ist, wie oben beschrieben, die Reaktion des Filters auf einen Dirac-Impuls.
Beispiel in Python:
import numpy as np
# Zeitparameter
sampling_rate = 1000 # Abtastfrequenz in Hz
t = np.linspace(0, 1, sampling_rate, endpoint=False) # Zeitvektor (1 Sekunde)
# Beliebiges Eingangssignal (z.B. eine Sinuswelle)
freq_input = 5 # Frequenz des Eingangssignals (z.B. 5 Hz)
input_signal = np.sin(2 * np.pi * freq_input * t)
# Beliebiges Filtersignal (z.B. ein Dreiecksignal)
filter_signal = np.concatenate([np.linspace(0, 1, 100), np.linspace(1, 0, 100)]) # Einfache Dreiecksform
filter_signal = np.pad(filter_signal, (0, sampling_rate - len(filter_signal)), 'constant') # Zero-Padding
# Faltung des Eingangssignals mit dem Filtersignal (native Berechnung)
output_signal = np.convolve(input_signal, filter_signal, mode='same') # 'same' sorgt für gleiche Länge wie Eingangssignal
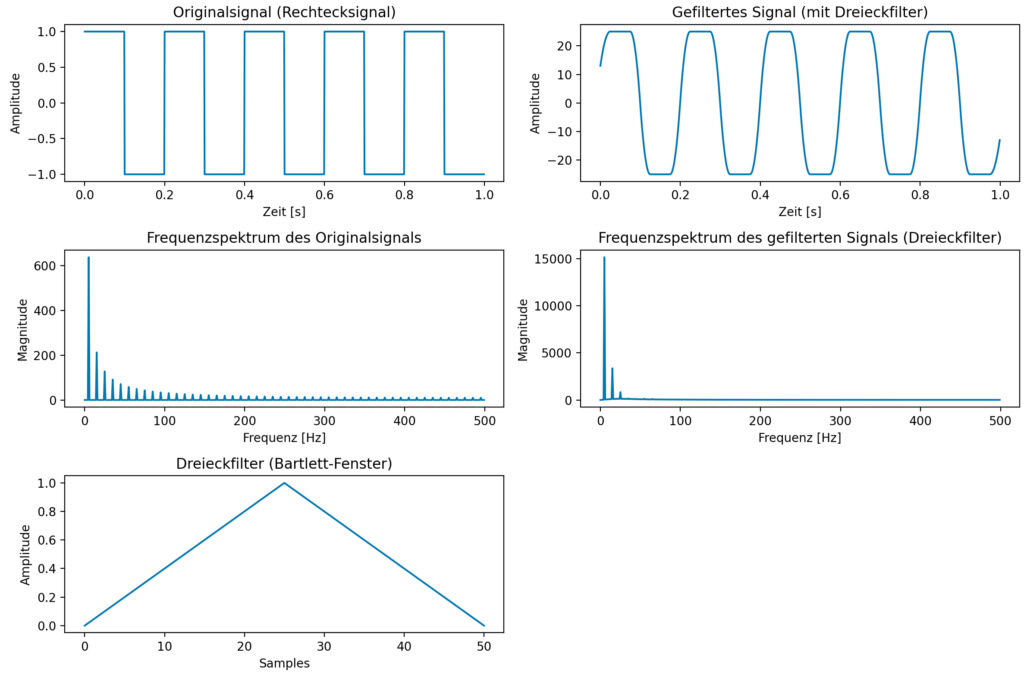
Ergebnis der Filterung
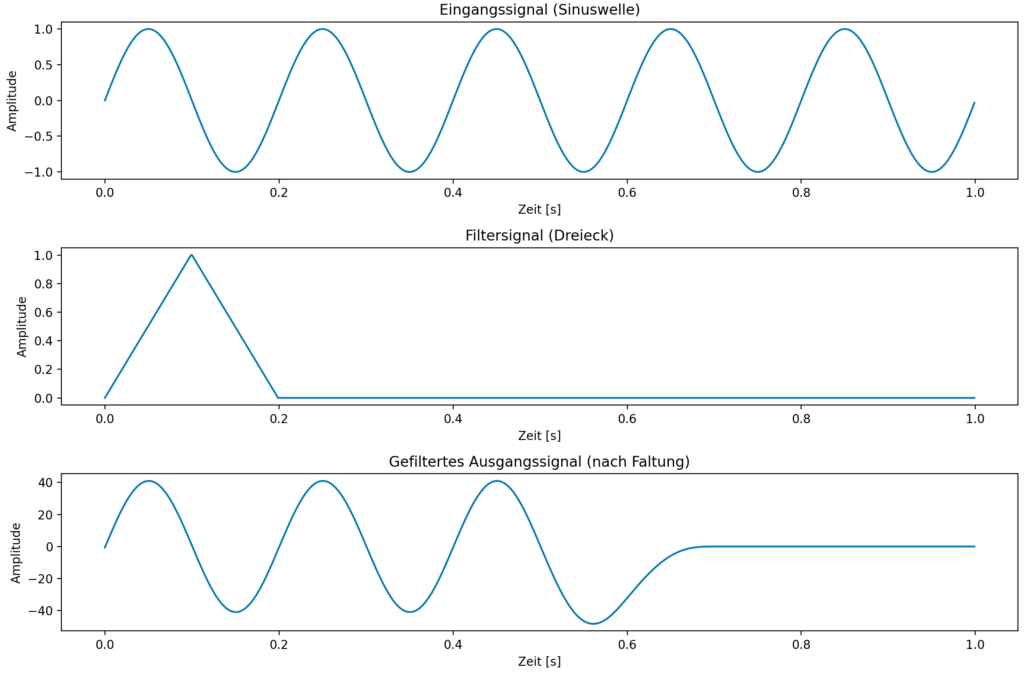
Bartlett Filter
Hier sind die jeweiligen Funktionen für ein Bartlett Filter dargestellt. Das Bartlett Fenster ist eine Dreiecksfunktion im Zeitbereich.
Das Bartlett Fenster gehört zu den sogenannten Fensterfunktionen. Die Implementierung dieser Funktion als einfacher Filter soll hier primär das Prinzip von Berechnungen in LZI Systemen aufzeigen.