Dieses Beispiel zeigt die Schritte, die zur Demodulation der mit DCF77 übertragenen Zeitinformation notwendig sind. Für die Demodulation wurde ein Signalausschnitt mittels KiwiSDR aufgezeichnet und als WAV Audio-Datei abgespeichert.
Das DCF77 Signal ist ein ASK Signal, das bei 77,5 kHz ausgesendet wird. Die WAV Datei wurde aber bereits ins Audio-Band verschoben und ist mit 44,1 kHz abgetastet.
Ein Audio-File ist daher ein Spezialfall, da die HF-Spannung bereits von 77,5 kHz auf eine hörbare Frequenz (oder direkt ins Basisband) herunter gemischt und nur auf eine, Kanal (Mono) aufgenommen wurde.
Ein Audio File enthält also nur den Realteil des ursprünglichen Signals. Wir wissen nicht, was im Imaginärteil passiert. Wenn wir nur den Absolutbetrag |x| der reellen Werte nehmen (was für die Demodulation des ASK Signals grundsätzlich ausreichend wäre) , erhalten wir eine sehr wellige Hüllkurve (da das Signal ständig durch Null geht). Der SDR Empfänger übernimmt normalerweise den Wandel des reellen Signals in ein IQ Signal. Diesen Schritt können wir auch mathematisch mit Hilfe der Hilbert Transformation erledigen.
Die Hilbert-Transformation berechnet zu jedem reellen Sample I den zugehörigen Imaginärteil Q. Sie ermittelt also, wie das Signal aussähe, wenn es um 90° phasenverschoben wäre. Als Ergebnis erhalten wir das komplexe IQ-Signal.
Das folgene Bild verdeutlicht den Unterschied. Die Hüllkurve des transformierten Signals ist wesentlich glatter als die des gleichgerichteten Realteils.
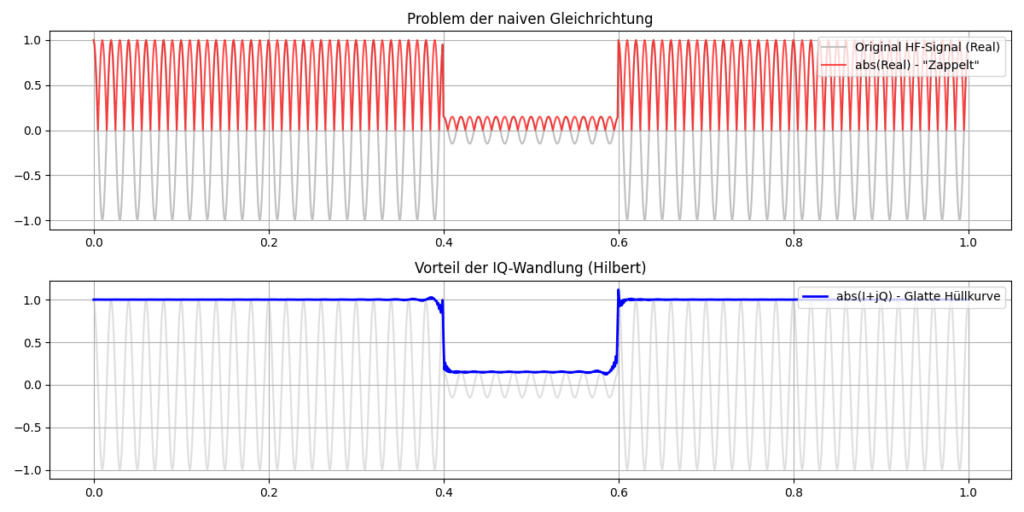
Die Gleichrichtung des Signals klappt die negativen Anteile des Signals einfach nach oben. Die Nulldurchgänge bleiben aber unverändert erhalten. Es wäre also zusätzlich erforderlich einen starken Tiefpassfilter zur Glättung einzusetzen, der das Signal zusätzlich verzerrt.
Da der Imaginärteil (Q) des Signals ist immer dann maximal ist, wenn I gerade Null ist (und umgekehrt) lässt sich der Betrag des komplexen Signals wie folgt berechnen:
Das Ergebnis ist eine perfekt glatte Linie.
Durch die IQ-Wandlung (ob in Hardware oder per Hilbert in Software) entfernen wir die Abhängigkeit von der Momentanphase des Trägers. Wir extrahieren die reine Energie des Signals. Für DCF77 bedeutet das: Wir sehen die 100ms/200ms Absenkungen, ohne dass uns die 77,5 kHz Schwingung dazwischenfunkt.
Aus der Hüllkurve können wir nun die digitalen Pulse ermitteln. Um echte Daten daraus zu machen, muss die Zeitdauer der Amplitudenabsenkungen (es handelt sich ja um ein ASK Signal) messen.
Beim DCF77-Signal ist die Logik einfach. Die für Standard-Funkuhren wichtigste Information steckt in der Amplitudenabsenkung. Einmal pro Sekunde wird die Amplitude des Trägersignals für eine kurze Dauer auf etwa 15 % des ursprünglichen Wertes abgesenkt.
Die Dauer dieser Absenkung bestimmt den logischen Wert des Bits:
Logisch 0: Absenkung für 100 ms.
Logisch 1: Absenkung für 200 ms.
Sekunde 59: In der letzten Sekunde jeder Minute erfolgt keine Absenkung. Dies dient als „Sync-Marke“, damit der Empfänger weiß, dass die nächste Absenkung den Beginn einer neuen Minute (Sekunde 0) markiert.
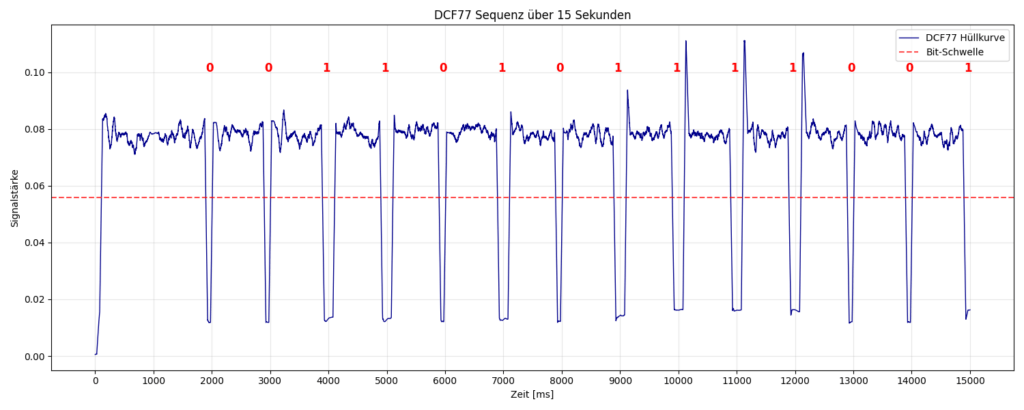
Im File sind mehrere Minuten enthalten. Die folgende Bitsequenz stellt einen Durchlauf von 59 Bits dar und liefert die Information zu einer Minute
Bit-Sequenz (59 Bits): 01101100111000100010100011101001010000010000110000011001000
Ergebnis: Do, 08.01.2026 - 14:38 Uhr
Code-Sprache: CSS (css)| Bereich | Bitsequenz | Wert | Bedeutung |
|---|---|---|---|
| 0-14 | 011011001110001 | – | Wetterdaten / Meteo Time (Verschlüsselt) |
| 15-19 | 00010 | MEZ | Rufbit (0), Zeitzone: MEZ (01), kein Schaltjahr-Aviso |
| 20 | 1 | Start | Beginn der Zeitinformation (Immer 1) |
| 21-27 | 0001110 | 38 | Minuten: 8+10+20 (BCD: Einer=8, Zehner=3) |
| 28 | 1 | P1 | Paritätsbit für Minuten (3 Einsen + 1 = Gerade) |
| 29-34 | 001010 | 14 | Stunden: 4+10 (BCD: Einer=4, Zehner=1) |
| 35 | 0 | P2 | Paritätsbit für Stunden (2 Einsen + 0 = Gerade) |
| 36-41 | 000100 | 08 | Kalendertag: 8 (BCD: Einer=8) |
| 42-44 | 001 | 4 | Wochentag: Donnerstag (1=Mo … 4=Do) |
| 45-49 | 10000 | 01 | Monat: Januar (BCD: Einer=1) |
| 50-57 | 01100100 | 26 | Jahr: 2+4+20 (BCD: Einer=6, Zehner=2 -> 2026) |
| 58 | 0 | P3 | Paritätsbit für Datum (4 Einsen + 0 = Gerade) |
Die ersten 15 Bit sind leider nicht decodierbar, da sie verschlüsselt sind. Das Rufbit hat aber eine wichtige Funktion im Bereich der Katastrophenwarnung. Wenn dieses Bit auf 1 ist, wird eine Katastrophenwarnung signalisiert, die in den ersten Bits näher beschrieben ist. Mit Hilfe dieses Bits werden Systeme des Katastrophenschutzes aktiviert.
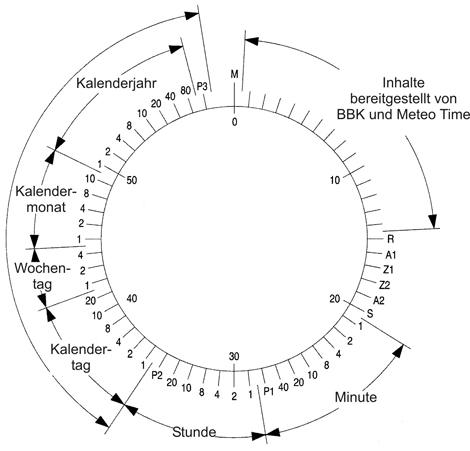
In dem Schaubild sind die einzelnen Bits noch einmal genauer Dargestellt. Tag, Monat und Jahr ist BCD Codiert gespeichert. Für Minute, Stunde und Datum ist zudem jeweils ein Paritätsbit enthalten. Die Anzahl der Einsen pro Gruppe muss zusammen mit dem P-Bit gerade sein.
Das folgende Python Programm führt die Analyse der WAV Datei mit dem DCF77 Signal aus.
Folgende Schritte sind dabei relevant:
- WAV Datei laden und Abtastrate bestimmen.
fs, data = wavfile.read(file_path)
if data.dtype == np.int16:
data = data.astype(np.float32) / 32768.0 - IQ Wandlung durchführen und Hüllkurve bestimmen.
Dieser Schritt übernimmt normalerweise der SDR Empfänger, wie ergänzen das Signal mathematisch. Die Hüllkurve ist mathematisch der Betrag der einzelnen Samples.
iq_signal = hilbert(data)
amplitude = np.abs(iq_signal) - Glättung durch Tiefpass Filter durchführen
window_size = int(fs * 0.05)
envelope_smooth = np.convolve(amplitude, np.ones(window_size) / window_size, mode=’same’) - Bestimmung der Impulse durch Ermittlung des Mittelwertes des Signals
threshold = (np.max(envelope_smooth) + np.min(envelope_smooth)) / 2
bits_raw = envelope_smooth < threshold - Erkennung der Flanken
changes = np.diff(bits_raw.astype(int))
rising_edges = np.where(changes == 1)[0]
falling_edges = np.where(changes == -1)[0] - Auswertung der Flankenänderungen und Erzeugung des Bitstromes
- BCD Dekodierung der Bitfolge
Hier ist das zugehörige Python Programm zur Auswertung des WAV Files.
from scipy.io import wavfile
import numpy as np
import matplotlib.pyplot as plt
from scipy.signal import hilbert
import datetime
def decode_dcf77(bits):
if len(bits) < 59:
return f"Unvollständig ({len(bits)} Bits)"
def bcd_decode(bit_slice, weights):
return sum(bit * w for bit, w in zip(bit_slice, weights))
try:
# 1. Uhrzeit
mins = bcd_decode(bits[21:28], [1, 2, 4, 8, 10, 20, 40])
hours = bcd_decode(bits[29:35], [1, 2, 4, 8, 10, 20])
# 2. Datum & Wochentag
day = bcd_decode(bits[36:42], [1, 2, 4, 8, 10, 20])
weekday_num = bcd_decode(bits[42:45], [1, 2, 4])
month = bcd_decode(bits[45:50], [1, 2, 4, 8, 10])
year = bcd_decode(bits[50:58], [1, 2, 4, 8, 10, 20, 40, 80])
# Wochentage Mapping
days_map = ["?", "Mo", "Di", "Mi", "Do", "Fr", "Sa", "So"]
weekday = days_map[weekday_num] if 1 <= weekday_num <= 7 else "?"
return f"{weekday}, {day:02d}.{month:02d}.20{year:02d} - {hours:02d}:{mins:02d} Uhr"
except Exception as e:
return f"Dekodierfehler: {e}"
# --- 1. Audio laden und Vorbereiten ---
file_path = "files/dcf77.wav"
print(f"Lade {file_path}...")
fs, data = wavfile.read(file_path)
if data.dtype == np.int16:
data = data.astype(np.float32) / 32768.0
# Falls es Stereo ist, nehmen wir nur den ersten Kanal (Mono)
if len(data.shape) > 1:
data = data[:, 0]
# --- 2. IQ-Wandlung & Hüllkurve ---
print("Erzeuge IQ-Signal via Hilbert-Transformation...")
iq_signal = hilbert(data)
amplitude = np.abs(iq_signal)
# Glättung (Lowpass) - 50ms Fenster
window_size = int(fs * 0.05)
envelope_smooth = np.convolve(amplitude, np.ones(window_size) / window_size, mode='same')
# --- 3. Puls-Extraktion ---
threshold = (np.max(envelope_smooth) + np.min(envelope_smooth)) / 2
bits_raw = envelope_smooth < threshold
# Flankenerkennung
changes = np.diff(bits_raw.astype(int))
rising_edges = np.where(changes == 1)[0]
falling_edges = np.where(changes == -1)[0]
# Sicherstellen, dass wir mit einer steigenden Flanke beginnen
if falling_edges[0] < rising_edges[0]:
falling_edges = falling_edges[1:]
# --- 4. Bit-Analyse & Zeit-Logik ---
print("Starte Bit-Analyse...")
# WICHTIG: Hier berechnen wir die Dauern aus den Flanken
num_pulses = min(len(rising_edges), len(falling_edges))
durations_samples = falling_edges[:num_pulses] - rising_edges[:num_pulses]
durations_ms = (durations_samples / fs) * 1000 # <--- Hier wird durations_ms definiert!
current_minute_bits = []
last_edge = 0
for i in range(num_pulses):
# Lücke zur vorherigen Flanke prüfen (Sekunde 59 Erkennung)
if i > 0:
gap = (rising_edges[i] - last_edge) / fs
if gap > 1.5:
bit_string = "".join(map(str, current_minute_bits))
print("-" * 60)
print(f"MINUTE VOLLSTÄNDIG (Synchronisationslücke erkannt)")
print(f"Bit-Sequenz ({len(current_minute_bits)} Bits): {bit_string}")
if len(current_minute_bits) >= 58:
zeit = decode_dcf77(current_minute_bits)
print(f"Ergebnis: {zeit}")
print("-" * 60)
current_minute_bits = []
# Puls-Dauer klassifizieren
d = durations_ms[i]
if 70 <= d <= 150:
val = 0
elif 170 <= d <= 280:
val = 1
else:
val = "?"
current_minute_bits.append(val)
# Ausgabe für jede Sekunde
print(f"Sekunde {len(current_minute_bits) - 1:02d}: Bit {val} ({d:3.0f} ms)")
last_edge = falling_edges[i]
# Den letzten Rest am Ende des Files auch noch ausgeben, falls vorhanden
if len(current_minute_bits) >= 58:
print(f"Letzte Minute im File: {decode_dcf77(current_minute_bits)}")
# --- 5. Finale Visualisierung (Optional) ---
plt.figure(figsize=(15, 6))
# Zeitraum definieren (in Sekunden)
seconds_to_show = 15
samples_to_show = int(seconds_to_show * fs)
# Zeitachse in Millisekunden erstellen
time_ms = (np.arange(samples_to_show) / fs) * 1000
# Plot der geglätteten Hüllkurve
plt.plot(time_ms, envelope_smooth[:samples_to_show],
label="DCF77 Hüllkurve", color='darkblue', linewidth=1)
# Schwellenwert einzeichnen
plt.axhline(y=threshold, color='red', linestyle='--', alpha=0.7, label="Bit-Schwelle")
# OPTIONAL: Automatische Bit-Markierung im Plot
# Wir suchen die Flanken im sichtbaren Bereich
visible_rising = rising_edges[rising_edges < samples_to_show]
for idx in visible_rising:
# Finde die dazugehörige fallende Flanke
corr_falling = falling_edges[falling_edges > idx]
if len(corr_falling) > 0:
duration = (corr_falling[0] - idx) / fs * 1000
bit_val = "0" if duration < 150 else "1"
# Text über den Puls schreiben
plt.text((idx / fs) * 1000, np.max(envelope_smooth)*0.9, bit_val,
fontsize=12, fontweight='bold', color='red')
plt.title(f"DCF77 Sequenz über {seconds_to_show} Sekunden")
plt.xlabel("Zeit [ms]")
plt.ylabel("Signalstärke")
plt.grid(True, alpha=0.3)
plt.legend(loc='upper right')
# x-Achse etwas schöner formatieren (Sekunden-Schritte markieren)
plt.xticks(np.arange(0, seconds_to_show * 1000 + 1, 1000))
plt.tight_layout()
plt.show()